Last Updated on 2023年12月28日 by カメさん

こんにちは!看護師のカメさん(@49_kame)です。
この記事は7~8分程度で読めます。

今回はオッズ比とリスク比について、オッズ比を中心に解説するよ。
研究結果で、要因の影響度の大きさを確認する際にオッズ比やリスク比などの言葉を聴いたことがあるのではないでしょうか。オッズ比やリスク比を理解して、研究結果を正しく理解しましょう。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。
リスク比・オッズ比とは?
リスク比・オッズ比とは?
- ある要因がある事象(結果)に対して関連があるかどうかを判断する際に使用する
- 横断研究や後ろ向き研究ではオッズ比
- 前向き研究ではリスク比
リスク比とは?
リスク比(Risk Ratio)とは?
- 相対危険度(Relative Risk)とも言う
- ある要因がある事象に対して関連があるかどうかを示す指標の1つ
- リスク比の特徴は前向き研究でしか使用できないこと
- リスク比が1以上になると、要因は結果に正の相関があることを意味する
- 値が大きくなると関連性が強くなる
リスク比の計算式は?
下記にリスク比の例を示します。要因のあり・なしの違いによって、疾患発生のあり・なしを前向きに調査した研究です。セルの中は人数です。

リスク比は、要因ありの中での発病率を要因なしの中での発病率で割ることで算出されます。少し難しいので図にしてみました。

リスク比は前向きの調査にしか使えない
このようにリスク比は、ある集団の中で何人が事象を起こすか(発病するか)の確率なので、前向きに観測される集団がなければ算出することができません。
オッズ比とは?
オッズ比(Odds Ratio:OR)とは?
- リスク比と同様に、ある要因とある事象(結果)の関係性を表す指標
- 要因が無いときに対して要因があった時は、結果が何倍起こりやすいかを表す
- オッズ比は横断研究や後ろ向き研究で使用できる
- 数値は0~∞の値を取る
- オッズ比が1の時は全く影響しない
- 1より大きくなるほど、1より小さくなるほど要因は結果(発病率)に相関があると判断する
オッズ比の計算式は?
オッズ比の例を示します。疾患のあり・なしによる要因の有無を、後ろ向きに調査した研究です。

つまり症例対照研究だね。

オッズ比は疾患ありの群の中の要因ありと要因なしの比を、疾患なしの群の中の要因ありと要因なしの比で割ることで算出されます。リスク比と同様に図にしてみました。
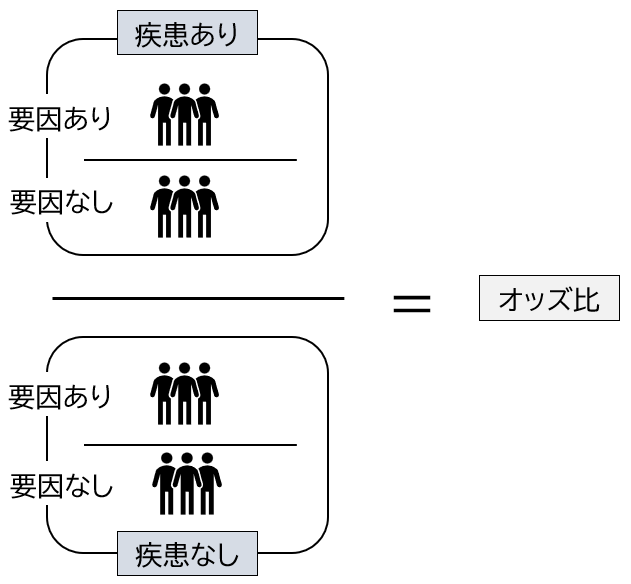
オッズ比は、独立変数の数値が1つ変化した時の倍率を意味します。そのため単純にオッズ比4だから4倍のリスクがあるという解釈は間違っているので注意してください。

ここからはオッズ比について詳しく解説していくいよ。
オッズ比はどうやって解釈するの?
オッズ比の解釈のポイントは?
- オッズ比が1の時は、良くも悪くも影響がない
- オッズ比は独立変数が1増加した時に従属変数が何倍起こりやすくなるか
独立変数が「量的変数」か「質的変数」かを判断する
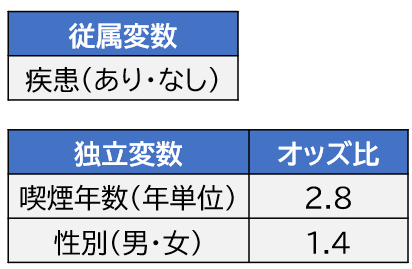
例えば、従属変数が疾患の有無、独立変数が①喫煙歴(年単位)と②性別(男・女)の場合で考えます。①喫煙歴のオッズ比が2.8、②性別のオッズ比が1.4という結果が算出されたと仮定します。
量的変数のオッズと質的変数のオッズをそれぞれ解説していきます。
量的な独立変数の時のオッズ比
独立変数①は年単位の喫煙歴です。つまり喫煙歴20年、30年などです。つまり量的な変数ですね。
オッズ比は「独立変数が1増えた時に従属変数が何倍起きやすいか」ですので、①喫煙歴が1年増えたということは、疾患が起きる危険が2.8倍という解釈になります。ちなみに、例えば喫煙歴が3年増えた時は、2.8³となるため疾患が起きる危険が21.952倍と解釈します。
質的な独立変数の時のオッズ比
独立変数②の性別は名義尺度という質的データです。「男・女」「ある・なし」のような質的データは0と1という数字のデータに変換します。

変換したデータをダミーデータと言うよ。
ダミーデータは「0・1」の2つの値のみのため、1だけ増加するということは「0→1」の変化ということです。つまり「男→女」、「あり→なし」の変化です。
先ほどの性別のオッズ比は1.4でした。ダミーデータの変換を男(0)・女(1)とすると、男性と比較して女性は1.4倍疾患になりやすいと解釈できます。
ダミーデータは必ずどちらが0でどちらが1かを確認しよう
ダミーデータの0と 1の割り当ては研究者が決定します。0と1を反対に解釈すると、逆数の結果となってしまいます。
ダミーデータを男0女1だと解釈していが実は男1女0だった場合を考えます。上記では女性だと1.4倍で疾患になりやすいと解釈しましたが、実は反対で1÷1.4(逆数)で女性だと0.71倍で疾患になりやすいという、まったく違う解釈になるので注意しましょう。
独立変数を組み合わせた場合の影響(オッズ比)も判断できる?
独立変数を組み合わせたオッズ比についても計算することができます。計算は簡単です。単純に独立変数同士のオッズ比を掛け合わせればOKです。
上記の例で考えます。喫煙歴が1年増加かつ女性だった場合、2.8×1.4=3.92倍疾患になりやすいと解釈できます。
オッズ比が1以下の時の解釈は?
オッズ比は0~∞の値を取るため、当然1以下になることもあります。その時の解釈について解説します。
上記の例で、喫煙歴のオッズ比が0.8だとします。その時は同様に喫煙が1年増加すると「0.8倍で疾患になりやすい」と解釈しますが、0.8倍と言われても分かりづらいです。そのため、0.8の逆数(1÷0.8)を取り「1.25倍で疾患になりにくい」と解釈します。

論文を読む時も、「従属変数の起こりやすさ」について述べているのか「従属変数の起こりにくさ」について述べているのかを理解しながら読み進めよう。
オッズ比の「95%信頼区間」の解釈は?
95%信頼区間とは?
統計解析の結果は信頼区間というものを考慮する必要があります。
95%信頼区間とは?
- 統計学において母集団がどのような数値の範囲にあるかを確率で示すもの
- 母集団の値(統計解析で推測しようとしている値)が、95%の確率で入る範囲(区間)を表す
- 複数の研究者が同じ研究をしたら、95%はこの範囲の値を取るだろうということ
オッズ比の95%信頼区間は?
オッズ比にも95%信頼区間があります。
オッズ比の95%信頼区間とは?
- オッズ比の95%信頼区間の下限が1より大きい(1.5ー3.5など)とき、統計学的に有意なオッズ比の上昇がある(要因と結果に有意な関連がある)と解釈する。
- 95%信頼区間の下限が1より大きいということは、95%の確率でオッズ比が1を上回ると推定される。つまり要因と結果に有意な関連がある可能性が95%以上ということ。
例えば「OR(オッズ比):2.4,95%CI(信頼区間):1.2ー3.8」などで表します。この時、95%信頼区間の上限が3.8、下限が1.2と考えます。もし95%信頼区間が0.8-1.4などの場合は有意な関連がありません。
下記の図は⇔が95%信頼区間です。①の95%信頼区間は有意な関連がなく、②の95%信頼区間は有意な関連があると解釈します。

95%信頼区間からオッズ比の精度も判定できる
95%信頼区間を見ることでオッズ比の精度も判定することができます。信頼区間の幅が狭いほど精度は高くなります。
オッズ比の精度を確認する計算は簡単で、オッズ比の95%信頼区間の下限値÷上限値です。基準は下記の図を参照してください。
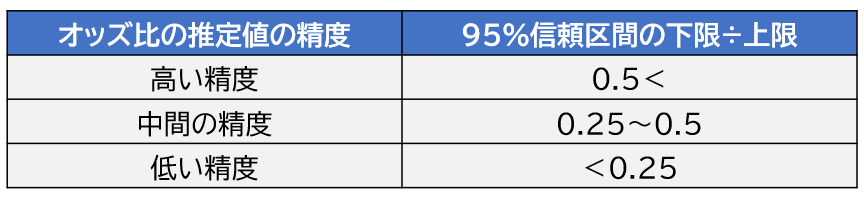
95%信頼区間が1.2-3.8だとすると、1.2÷3.8=0.31・・。つまり、中程度精度であることが分かります。
実際の論文のオッズ比を見てみよう
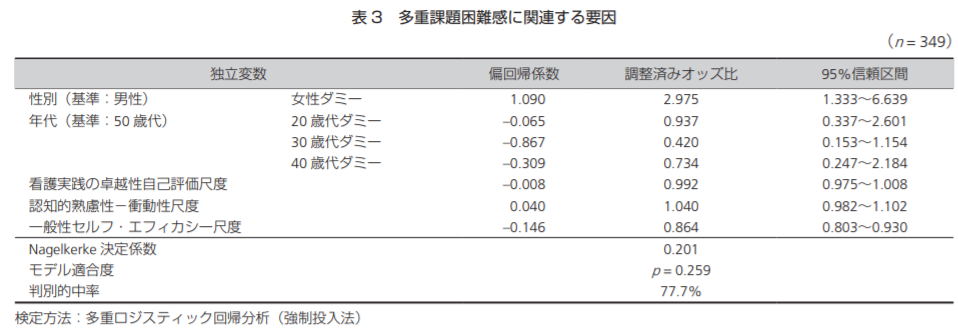
この論文は看護師の多重課題困難感の要因を調査した研究です。従属変数を多重課題困難感の有無として要因を調査しています。
オッズ比は?
1番上の性別のオッズ比を基に解説します。ダミーデータは男性を基準0としているので、男性が0、女性が1です。このオッズ比は独立変数である男性(0)→女性(1)に変化したときの従属変数の起こりやすさを示しています。つまり男性と比較して女性は多重課題困難感を感じる可能性が高いという結果です。

従属変数は多重課題困難感を「感じない」が0、「感じる」が1だよ。今回の多変量解析では0→1の変化、つまり「感じない」から「感じる」が起こることに影響する独立変数を検討しているよ。
オッズ比の95%信頼区間は?
性別のオッズ比の95%信頼区間も見てみましょう。1.333~6.639と記載しています。下限が1以上なので有意な関係があると判断できます。推定の精度は下限÷上限で0.2なので、あまり精度が高いとは言えません。
その他の独立変数に関しても同様の解釈で問題ありません。有意な関係性を示しているものは少ないですが。年代のダミーデータについても20歳代ダミーのオッズ比を解釈するのであれば、「20代ならば○○倍多重困難感を感じやすい」という解釈です。

前にも伝えた通り、ダミーデータの基準の0がどちらに設定されているかを必ず確認してから解釈するように注意しよう!
まとめ

オッズ比を中心に解説しました。リスク比もオッズ比も要因と結果の関連性の強さを示したものです。
オッズ比は独立変数が1増えた時の従属変数が何倍起きやすいかの指標です。独立変数が量的データなのか、質的データなのかを確認し、1増えるということが何を表すのかを確認しましょう。
またオッズ比やリスク比の数字だけに注目せず、結果に示された数字が臨床的にどの程度の意味を持つのかを念頭に置きながら解釈しましょう。
この記事を読んだ方におすすめの書籍を下記で紹介しています。良かったら参照してください。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。
引用・参考文献
- 対馬栄輝(2020).医療統計解析使いこなし実践ガイド.羊土社,東京.
- 内田治,石野裕三子,平野綾子(2018).JMPによる医療系データ分析-統計の基礎から実験計画・アンケート調査まで-第2版.東京図書,東京.
- 対馬栄輝(2019).医療系研究論文の読み方・まとめ方.東京図書,東京.

















コメント