Last Updated on 2024年3月30日 by カメさん

こんにちは!看護師のカメさん(@49_kame)です。

今回はカイ二乗検定を含む、分割表の検定について説明していきます。
カイ二乗検定という名前は、看護師の研究でも使われることがよくあるので、皆様も耳にしたことがあるのではないでしょうか。クロス集計表や分割表という言葉も良く聞く言葉ですね。なんとなく聞いたことあるけど、どんな解析方法か分からないという方が多くいると思うので、分かりやすく解説していきます。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。
カイ二乗検定とは?
カイ二乗検定とは、分割表の検定と呼ばれる解析方法の中の一つの方法です。
分割表の検定とは?
- 分割表の検定は2つの変数について解析する
- 分割表の検定にはカイ二乗検定(正確にはカイ二乗独立性の検定)とFisherの正確確率検定の2つに分けられる
t検定となにが違うの?

2つの変数を扱うという意味ではt検定と似ているね。
t検定と大きく違うところは、扱う尺度(データの種類)です。t検定では比率尺度や間隔尺度などの量的データを使用します。
分割表の検定では、名義尺度や順序尺度といったカテゴリカルデータ(質的データ)を使用します。
カテゴリカルデータ(質的データ)・量的データとは?
- 質的データとは名義尺度(男性や女性などの分類のみに意味があるデータ)や順序尺度(重症度など、分類に加えて順序にも意味があるデータ)のことです。
- 量的データとは、間隔尺度や比率尺度といった間隔や比率に意味のあるデータで計算ができます。
- 質的データは四則演算ができないという特徴があります。
尺度についての詳しい内容は下記の記事を参照してください。
「分割表(クロス集計表)の検定」とは?
分割表の検定とは?
行と列にそれぞれ変数(列が性別で行が疾患など)を置いて、変数毎の人数を分析する方法
分割表(クロス集計表)の例を以下に示します。
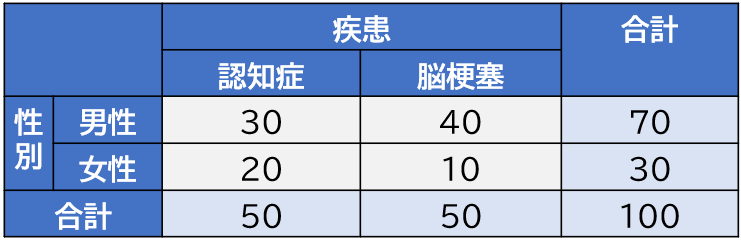
今回は2×2の表を示しましたが、2×3の表なども使用できます。例えば行の疾患を3つに増やすなども可能です。
今回は列(縦)の変数が性別で行(横)の変数が疾患名です。そしてそれぞれの変数が2つのカテゴリー(男性・女性とか)を持っています。

列は「れ」の書き順が縦からだから縦の列。
行は「ぎ」の書き順が横からだから横の行。
と覚えるといいよ!
セルの中がそれぞれの人数です。
この表を見ると、なんだか性別と疾患に関連がありそうですよね。それを統計的に確認するのが分割表の検定です。
「分割表の検定」の流れ
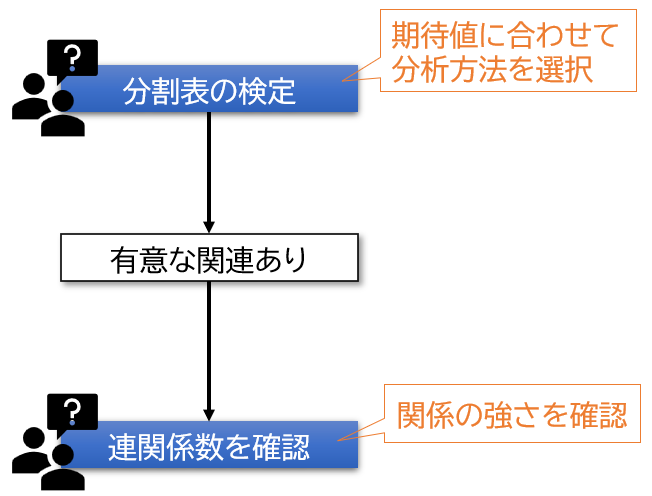
分割表の検定(分析方法の選択は下記参照)を行った後、有意な関連を認めた場合は、連関係数を確認します。
連関係数とは変数間の関係の強さを確認するものです。
詳しくは下記の「連関係数とは?」の項を参照してください。
「分割表の検定」の分析方法を選択する

分割表の検定は他の統計解析みたいに正規分布の確認とかはしなくて大丈夫だよ。
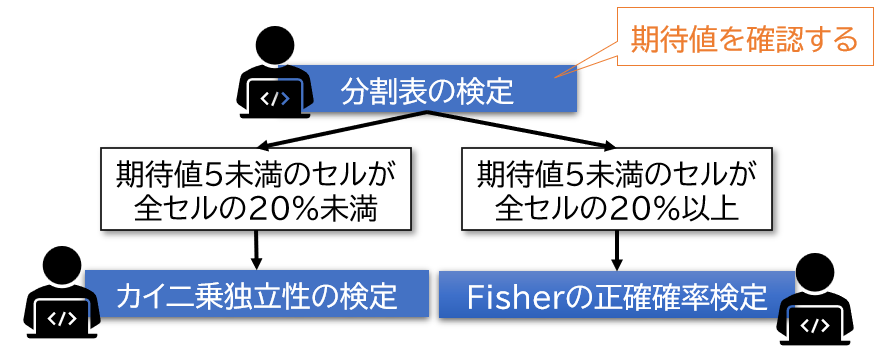
分割表の検定を使用する際は、期待値の状況によって、カイ二乗独立性の検定を使用するかFisher(フィッシャー)の正確確率検定(or Fisherの直接確率法)を使用します。
期待値の状況とは?
期待値の状況とは、期待値が5未満のセルがどのくらいあるかです。

期待値が5未満というのは、データが少ないということだよ。
統計ソフトで解析すると、度数表と期待値の表が提示されるので、期待値の表を確認して判断しましょう。
期待値が5未満のセルが20%未満の場合(2×2の分割表だと5未満のセルが無い)は、カイ二乗独立性の検定を適用します。
期待値が5未満のセルが20%以上存在する場合(2×2の分割表だと1つ以上のセル)は、Fisher(フィッシャー)の正確確率検定カイ二乗独立性の検定を適用します。
「分割表の検定」における期待値とは?
期待値とは?
- 変数同士にまったく関連がないとしたときのセルの値
- 期待値は、算出したいセルの列合計×行合計÷総合計で算出される

上記図の左上のセル(度数が30)を例にします。A1の列合計50、B1の行合計50、総合計100とすると、期待値は セルの列合計(50)×行合計(50)÷総合計(100)= 25になります。この例は行合計と列合計が同じなので、4つのセルの期待値は全て25になります。
つまり、期待値(変数同士にまったく関連がない場合のセルの値)とは行合計、列合計を加味した上で総合計を均等に各セルに配置した値です。

列合計20・行合計20などのデータが少ないセルが期待値5未満になりそうだね。
最初に示した分割表の期待値を見てみましょう。

認知症の列合計が50、男性の行合計が70、総合計が100でした。先ほどの計算式で計算すると左上のセルの期待値は35になります。つまり期待値が35、度数(実際の人数)が30と分かります。
分割表の検定では、この期待値と実際の値の差を分析して差が大きければ有意な関連があると判断します。
分割表の検定では期待値と実際の人数の差を分析することで、変数同士に関連があるかを解析する。
「連関係数」で変数間の関係の強さを見る
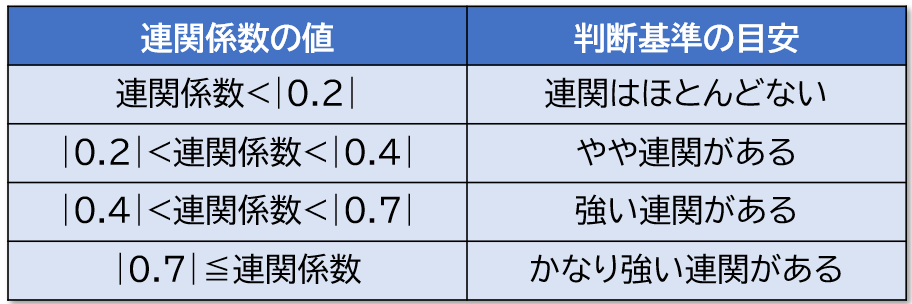
分割表の分析にて2つの変数間に有意な関連があると分かったら、次に変数間の関連の強さを連関係数という指標を算出して確認します。相関係数と考え方は同じです。
連関係数の関係の強さについては、目安を示しますので参考にしてください。この目安についても相関係数とほぼ同じです。
「連関係数」の選択方法
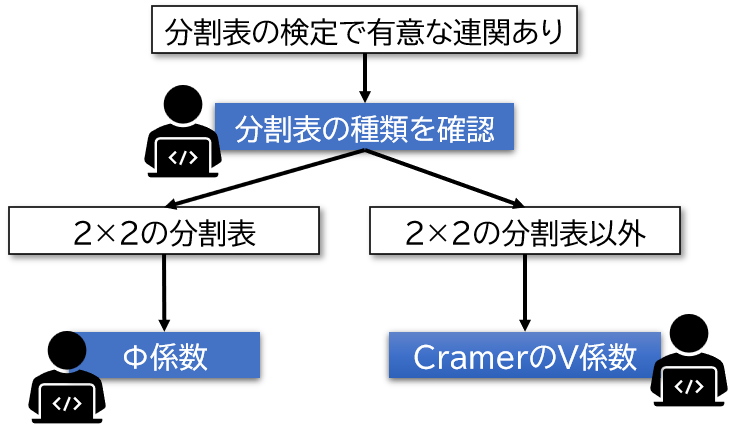
連関係数は一般的に2つの係数があります。
上記の分割表の例で示したような2×2の分割表の場合はφ(ファイ)係数を使用します。
2×2以外の分割表の場合(2×3や3×3など)はCramer(クラメール)のV係数を使用します。
どちらも0~1の値を取ります

φ係数は-1~1の値を取る場合もあるよ。
相関係数と同じ解釈、で0に近い程関係が小さく、1に近いほど関係が強いと判断する
「分割表の検定」の結果の解釈
変数同士の関連は?
変数間の関連を確認するには、カイ二乗独立性の検定やFisher(フィッシャー)の正確確率検定 の結果を確認します。
「カイ二乗独立性の検定の結果、p<0.05で、性別と疾患に有意な関連を認めた」
どのセルの度数(人数)が多くて?どのセルが少ない?
どのセルの度数が有意に多くて、どのセルが有意に少ないかは、調整済み残差という数値を確認します。

度数とは、人数とかの標本数のことだよ。
「認知症の男性が調整済み残差1.96以上で有意に多い」
調整済み残差とは?
- 期待値ー度数(実際の人数)が残差と呼ばれ、それを調整したもの。
- 期待値からのズレが大きいほど残差も大きくなる。
- 数値が1.96以上の時は有意に大きく、-1.96以下の時は有意に小さい。
変数間の関連の強さは?
関連の強さは上記に示した通り、連関係数を用います。
「φ係数が0.46で強い連関がある」
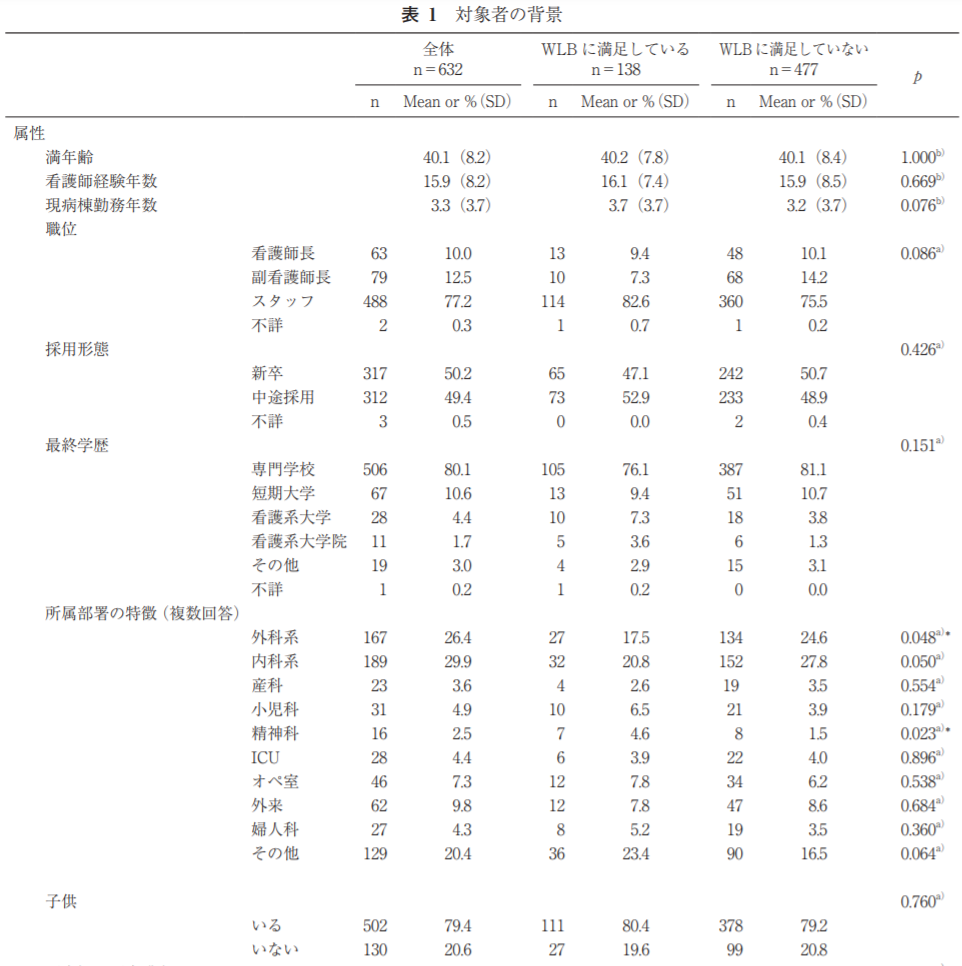
実際の論文での分割表の検定を紹介
今回紹介する論文は既婚女性のワークライフバランスの満足度について関連情報(基本情報や尺度など)との関係を見ながら分析した研究です。
以下にこの研究の表を提示します。
右端のp値でa)と書かれているものがカイ二乗検定の結果、b)マンホイットニーU検定の結果です。
学歴や子どもの有無など、質的データ(カテゴリカルデータ)にはカイ二乗検定を使用し、尺度の値や勤務時間など量的データにはマンホイットニーU検定を使用しています。

この研究のように、研究で扱うデータ毎に複数の解析方法を組み合わせることが良くあるよ。
論文を読む際は、研究ではどのようなデータを扱っていて、そのデータに対してどのような分析をしたのかという視点で読むようにしてくみましょう。
まとめ

カイ二乗検定は、分割表検定のうちの一つで、質的データを分析することができる検定方法です。
質的データであっても統計解析をすることができます。論文を読む上で、大事なことは統計解析に使用したデータの種類を理解することです。
解析結果だけではなく、どんなデータをどのような解析方法を使用したのかという全体像を把握するようにしましょう。
この記事を読んだ方におすすめの書籍を下記で紹介しています。良かったら参照してください。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。
引用・参考文献
- 対馬栄輝(2020).医療統計解析使いこなし実践ガイド.羊土社,東京.
- 対馬栄輝(2019).医療系研究論文の読み方・まとめ方.東京図書,東京.
- 前田 樹海(2015).この1冊でできる! はじめての看護研究.ナツメ社,東京.

















コメント