Last Updated on 2024年3月30日 by カメさん

こんにちは!看護師のカメさん(@49_kame)です。
この記事は10分程度で読めます。

今回は、変数同士の因果関係を検討する統計手法について解説します。
- 統計解析に苦手意識がある
- 因果関係を明らかにしたい
- (重)回帰分析の結果の読み方を知りたい
- (重)回帰分析の概要を知りたい
多変量解析については苦手意識がある人が多いと思いますが、分かりやすく解説できるように努力するのでよろしくお願いします。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。
回帰分析ってなんのこと?
回帰分析とは?
独立変数が従属変数に及ぼす影響を分析する手法
つまり、原因(独立変数)と結果(従属変数)の関係を分析する手法です。
相関分析と混同される方がいますが、相関分析は二つの変数の関係のみを分析しており、回帰分析は2つの変数の因果関係を分析しています。
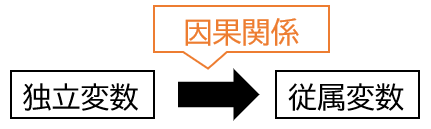
独立変数:
- 目的変数を説明するため、説明変数とも呼ぶ。
- 物事の原因と捉えることができる。
従属変数:
- 独立変数から予測したい変数のこと。
- 目的変数や外的基準とも呼んだりする。
- 物事の結果と捉えることができる。
単回帰分析・重回帰分析ってなに?
単回帰分析とは?
- 従属変数に対して独立変数が1つの場合
重回帰分析とは?
- 従属変数に対して独立変数が2つ以上の場合
- 重回帰分析は多変量解析の1つ

多変量解析とは、複数の変数間の関係性を分析する手法の総称だよ。
回帰式ってなに?
回帰分析の特徴は、回帰式を作成することです。
回帰式とは?
- 独立変数と従属変数の関係を表す関係式のこと。
- 単回帰分析ではy=a+bx 重回帰分析ではy=a+b₁x₁+b₂x₂・・・
回帰式は下記の散布図の真ん中に引かれている線のことです。
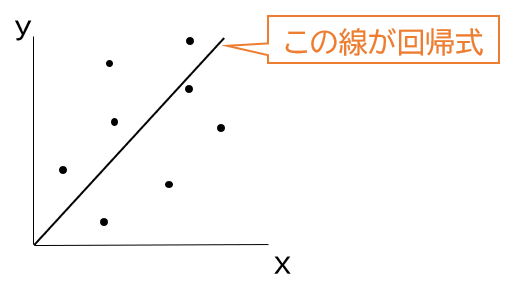

実測値(散布図の中の点)からの距離が最も小さくなるように作成されているよ。
回帰式のXとかYってなんのこと?
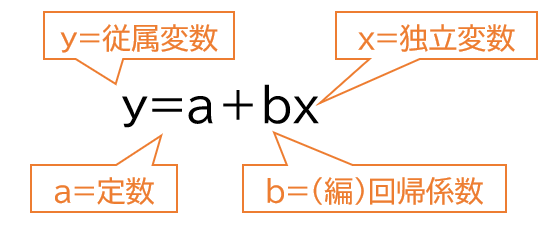
X:独立変数
y:従属変数
a:定数
b:単回帰分析ではあれば回帰係数、重回帰分析であれば編回帰係数
標準回帰係数・標準編回帰係数ってなに?
標準回帰係数・標準編回帰係数とは?
- 単回帰で標準回帰係数、重回帰で標準編回帰係数を使用する。
- 独立変数xが従属変数yに与える影響の大きさを判断できる値。
- 0~±1の値を取る。
- ±1に近いほど強い影響がある。

回帰係数bは、yやxの単位によって値が異なるよ。だから、回帰係数ではなくて標準(編)回帰係数を求めて独立変数の影響の大きさを確認するよ。
下記に標準(編)回帰係数の影響力の目安を示します。相関係数のようにあくまで目安なので参考までに確認してください。
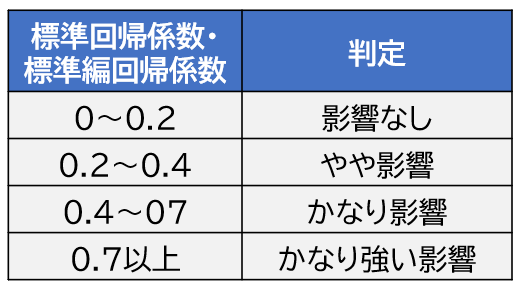

下記で説明する多重共線性の影響で値が±1を超えることもあるから注意が必要だよ。
決定係数R²ってなに?
決定係数R²とは?
- 回帰式の予測精度・影響の大きさを表す。
- 0≦R²≦1の範囲を取る。
- 1に近づくほど回帰式の予測精度が高い。
R²>0.5であれば回帰式の適合が良いとされます。つまり予測精度が高いということです。
しかし、これはあくまで目安なので低いから問題というわけではありません。

決定係数R²は寄与率と言われることもあるよ。
独立変数は全て分析できるわけではない
多重共線性の問題
重回帰分析では、複数の独立変数を組み込むことで従属変数に与える要因を検討します。
多重共線性とは?
複数の独立変数間に高い相関がある場合に適切な結果が出ない状況のことです
多重共線性には基準がある
- 各独立変数間の相関係数が≧0.9であった場合に多重共線性があると判定する
- 分散拡大要因(VIF)>10で多重共線性ありと判定する
VIFとは?
編回帰係数の値の不安定性や信頼性の低さを表す尺度

相関係数もVIFもどちらも統計ソフトにより出力されるので確認しよう。
多重共線性ありと判定された場合の対応
相関行列表を作成し、相関の高い変数のどちらか一方を取り除いてから再度解析を行います。
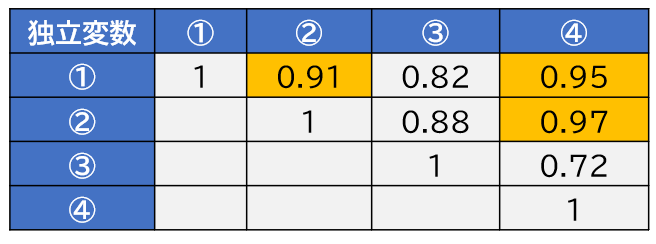
例えば、r≧0.9が3つ(変数①②④)存在する場合はこれらの3つの変数からどれか1つを選んで使用する必要があります。
変数選択法とは?
変数選択法とは?
重回帰分析のような複数の独立変数を扱う時に適切な独立変数を選択する方法
なるべく少数の独立変数で説得力のある回帰式とすることが推奨されています。
変数選択法には以下のような方法がありますが、最も効率が良いのがStepwise法であり、おすすめです。
変数選択法には種類があるの?
すべての独立変数を投入して重回帰式を作る
既存の重回帰式に新たな変数を追加していく
既存の重回帰式から変数を減少させていく
1つずつ独立変数を入れたり抜いたりしながら最適なモデルを探索する

変数選択法は統計ソフトにあるから安心してね
必要な変数は強制投入しよう
変数選択法だけで独立変数を決定してしまうと、臨床的に意味のある変数が抜けてしまうことがあります。臨床経験の基、従属変数に影響を与えると思われる変数は強制投入しましょう。
回帰分析の4つの手順
単回帰分析も重回帰分析も本来はパラメトリックな手法ですが、一般的には分布を問わず同様の手法で行われているため正規性の確認は必要ありません。
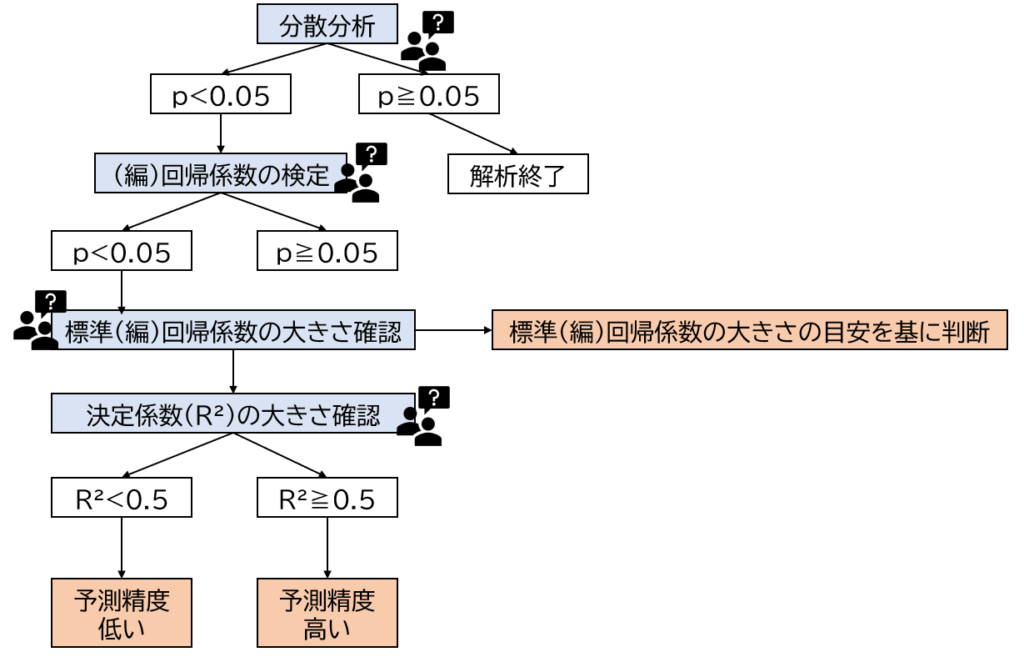
①分散分析
まずは回帰分析においても分散分析を行います。
分散分析では回帰式が役に立つかどうかを判断します。
つまり、p<0.05ならば役に立つ回帰式。p≧0.05ならば役に立たない回帰式と判断します。p≧0.05ならば、この時点で解析終了となります。

分散分析を行わない研究も良く見かけるね。
②回帰係数の検定
(編)回帰係数の検定では、それぞれの独立変数が役に立つかどうかを判断します。
p>0.05であれば各独立変数は役に立つと考えます。

ちなみに定数(回帰式のa)は有意性を考える必要はないよ。
③標準(編)回帰係数の大きさを確認
前述した通り、標準(編)回帰係数は独立変数が従属変数に与える影響の大きさです。
上記の目安を参考に影響度を解釈しましょう。
④決定係数(R²)の大きさを確認
前述の通り、決定係数とは回帰式の予測精度・影響の大きさです。
解析した回帰式の決定係数(R²・寄与率)を確認し、回帰式の予測精度を解釈しましょう。
変数選択法による結果以外の結果も考慮しよう
変数選択法により、従属変数に影響を与えている独立変数が除外されることがあります(独立変数の少ない回帰式を作るために)。変数選択後の回帰式の結果だけではなく、従属変数と独立変数の相関や、独立変数毎の相関、1変数毎の回帰式を参考に結果を解釈するようにしましょう。
実際の論文を見てみよう
論文の概要
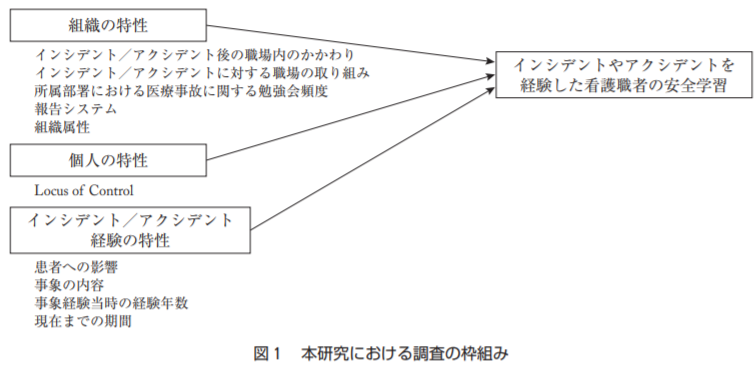
これは、インシデント・アクシデントを経験した看護師の安全学習に関連する要因つまり因果関係を調査した研究になります。
概念枠組みでは従属変数が安全学習、独立変数が組織的要因、個人的要因、インシデント・アクシデントの経験になります。
分析方法
この論文では、分析方法を1次分析・2次分析・3次分析に分けています。
- 1次分析:記述統計と正規性の確認
- 2次分析:分散分析・相関分析・2標本の分析
- 3次分析:重回帰分析
ポイントは、3次分析における独立変数の選択です。
独立変数は2次分析で有意であったもの+変数増減法(Stepwise法)により選択されています。
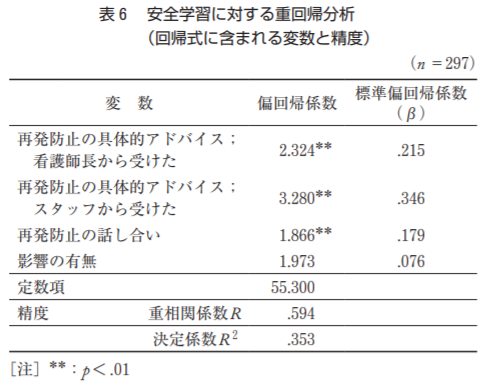
重回帰分析の結果
編回帰係数の検定
左に記載されているのが独立変数です。上記3つの**がついているのが有意な独立変数ということです
標準編回帰係数の大きさを確認
有意な独立変数を確認すると、標準編回帰係数は0.179~0.346の間の値のため、目安を基に考えると各独立変数は影響なし~やや影響ありの間の影響度ですね。
決定係数(R²)の大きさを確認
R²は0.353であり予測精度は低い結果であることが分かります。
多重共線性等についての記述は見当たりませんでした。

今回は統計的に有意な変数のみ投入していますが、臨床家として必要だと思う変数を追加で投入することもあるよ。
紹介した論文についての個人的見解
今回紹介した論文について、標準編回帰係数の大きさや回帰式の予測精度についての言及はありませんでした。また、看護師長とスタッフからアドバイスの影響度の差について考察されていますが、標準編回帰係数で見ると大きな差がないため、どこまでこの差について言及できるかは難しいところだと思います。
筆者の考察を否定しているわけではありません。1つの結果でも複数の視点があると思います。読み手が結果を正確に読み取り客観的に解釈するということが重要だと考えます。
まとめ

重回帰分析に難しいイメージを持っている人は多くいると思います。しかし、ポイントを理解すれば難しいものではありません。
大事なことは、重回帰分析の結果だけではなく複数の統計解析結果や臨床経験を踏まえて結果を解釈することです。色々な解析方法を使って多面的に追及していきましょう。

難しい解析方法を使えば良いというわけじゃないよ。目的を整理しながら、適した解析方法を複数使って解釈しよう!
この記事を読んだ方におすすめの書籍を下記で紹介しています。良かったら参照してください。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。
引用・参考文献
- 対馬栄輝(2020).医療統計解析使いこなし実践ガイド.羊土社,東京.
- 対馬栄輝(2019).医療系研究論文の読み方・まとめ方.東京図書,東京.















コメント