Last Updated on 2024年3月30日 by カメさん
こんにちは！看護師のカメさん(@49_kame)です。
この記事は10分程度で読めます。
今回は多変量解析の１つである多重ロジスティック回帰分析について解説するよ
- 統計解析に苦手意識がある
- 因果関係を明らかにしたい
- 多重ロジスティック回帰分析の結果の読み方を知りたい
- 多重ロジスティック回帰分析の概要を知りたい
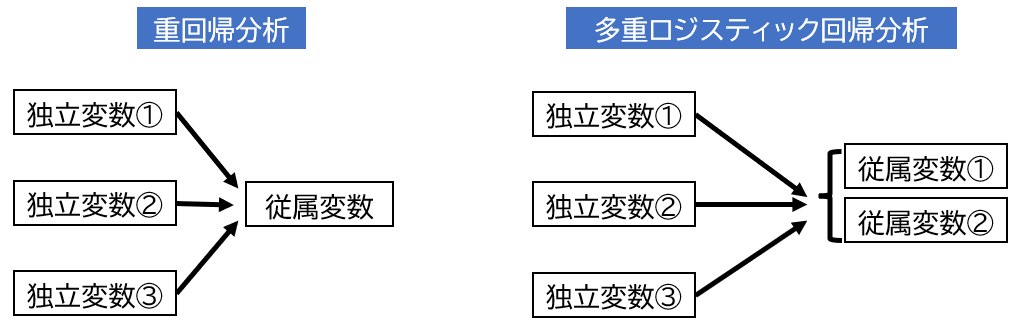
多重ロジスティック回帰分析とは、重回帰分析と同様に、独立変数から従属変数を予測する分析方法です。
重回帰分析については詳しく知りたい方は下記を参照してください。
研究では統計解析のために膨大なデータ（アンケート調査のデータなど）を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも１つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!（エミーオ）がおすすめ！で紹介しているので良かったら参照してください。
多重ロジスティック回帰分析とは？
多重ロジスティック回帰分析とは？
複数の独立変数が従属変数に与える影響を調べる方法
独立変数：
- 目的変数を説明するため、説明変数とも呼ぶ。
- 物事の原因と捉えることができる。
従属変数：
- 独立変数から予測したい変数のこと。
- 目的変数や外的基準とも呼んだりする。
- 物事の結果と捉えることができる。
多重ロジスティック回帰分析の良いところは？
多重ロジスティック回帰分析の良いところは？
制約となる条件がほとんどないため、データの条件を気にすることなく解析できる
解析したいデータを何も気にせず解析することができるよ。
いままでの解析手法と異なり、データの正規分布や、質的データ・量的データなどの条件がありません。
解析手順や結果の解釈については決められた手順で行う必要がありますが、前提条件がなく扱いやすいため看護師の研究でも多く使われています。
重回帰分析と多重ロジスティック回帰分析の違いは？
重回帰分析と異なる点は？
従属変数が2値データであるということ
2値データ
- 0－1型データ、ダミー変数などと呼ばれる
- 「疾患あり・なし」、「学習能力が高い・低い」など
重回帰分析は1群の従属変数に対して、複数の独立変数の影響を分析する方法でした。
多重ロジスティック回帰分析は2群の従属変数（疾患あり・なしの差）に対して、複数の独立変数の影響を分析する方法です。
2群の差にt検定を使わない理由「交絡因子の検討」
2群の従属変数の差を検定するのであれば、対応のないデータなので、もちろんt検定でも問題ありません。しかし、交絡因子の問題を検討しなければいけません。
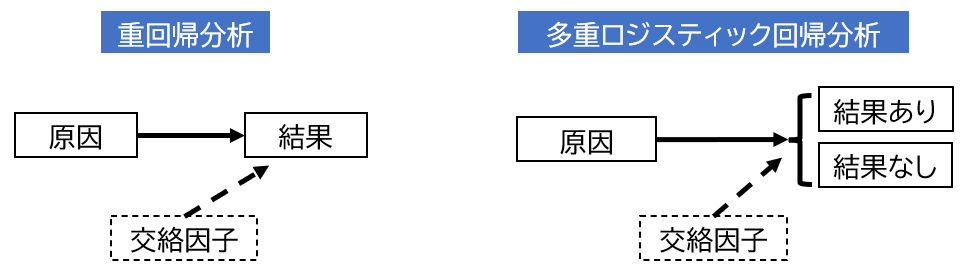
交絡因子とは？
- 原因と結果が存在する時に背後に存在する要因
- つまり結果には原因だけでなく交絡因子が影響していたかもしれないということ
2標本のt検定では、「喫煙年数に対する疾患あり・なし（独立した2群）の差」等を比較しました。原因と結果に置き換えると疾患あり・なしが従属変数であり、喫煙年数が独立変数です。
疾患あり・なしには喫煙年数以外にも背景的な要因がありそうですよね。これが交絡因子です。t検定では交絡因子を考慮することができません。
交絡因子を考慮して解析できるのが多重ロジスティック回帰のような多変量解析だよ
多変量解析とは？
- 複数の変数間の関係性を分析する手法の総称
- 同時に複数の変数が関連し合う状態（交絡因子）を考慮しながら、各独立変数の従属変数への影響を分析できる
独立変数の影響の大きさを確認！オッズ比とは？
多重ロジスティック回帰分析では独立変数の影響をオッズ比にて確認します。
オッズ比とは？
- 危険率を表す指標
- 原因が無いときに対して原因がある時は、結果が何倍起こりやすいか倍率で表す
- 数値は0～∞の値を取る
- オッズ比が1の時は全く影響せず、1より大きくなるほど、1より小さくなるほど影響（倍率）が大きいと判断する
横断研究や後ろ向き研究ではオッズ比、前向き研究ではリスク比となります。
横断研究などの研究デザインについて詳しく知りたい方は下記を参照してください。
オッズ比は「独立変数の数値が1つ変化した時の従属変数の起こりやすさ」の倍率を意味する。オッズ比が4だから4倍のリスクがあるという解釈が間違っているから注意。
オッズ比についての詳しい解説を知りたい方は以下の記事を参照してください。
ダミー変数とは？質的データを独立変数に投入したい
ダミー変数とは？
- 量的な統計解析の際に、独立変数に質的データを投入したい場合に使用する
- 質的データを0－1のダミー変数へと変換する。
看護師の研究では、量的変数と質的変数が混在することは良くありますのでダミー変数を覚えておくと便利です。例えば、男女の違いを独立変数として投入したいと考えた場合は、男が0、女が1と変換して量的データとして分析します。
基準となる0は研究者が決めるため、ダミー変数を用いた論文を読む際は結果の解釈に注意が必要。結果を読む前にダミー変数の基準0を確認する。
ダミー変数について詳しく知りたい方は下記のリンクを参照してください。
多重ロジスティック回帰分析の3つの手順
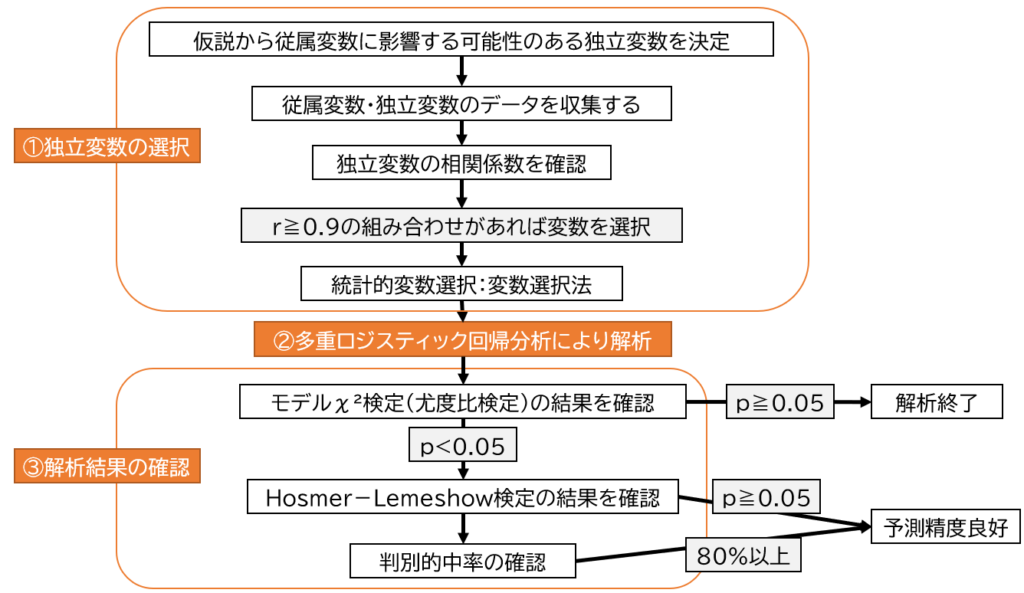
①独立変数の選択
仮説を基に独立変数を検討する＆データを収集する
多変量解析の良い点は複数の独立変数を検討できる点です。しかし、なんでもかんでもデータを収集するのはよくありません。
徹底した文献検討により仮説を立てた上で独立変数を検討しましょう。
独立変数とサンプルサイズには関係がある
- 多変量解析では、独立変数の数は、ｎ数に応じて決定する必要がある
- ｎ数÷10までの独立変数が望ましい（ｎが100であれば、独立変数は10まで）
- ｎ数に比べて独立変数が多くなると、回答が極端にすくない独立変数が存在してしまう。偏った変数が存在すると正常な解析ができなくなる。
収集した独立変数から解析に使用するものを選択する
多重共線性を考慮した変数選択
重回帰分析と同様に独立変数を選びます。独立変数を選ぶ際は多重共線性を考慮する必要があります。
多重共線性とは？
複数の独立変数間に高い相関がある場合に適切な結果が出ない状況のことです
多重共線性には基準がある
- 各独立変数間の相関係数が≧0.9であった場合に多重共線性があると判定する
- 分散拡大要因（VIF）>10で多重共線性ありと判定する
VIFとは？
独立変数の影響を確認する値の不安定性や信頼性の低さを表す尺度。
相関係数もVIFもどちらも統計ソフトにより出力されるので確認しよう。
多重共線性ありと判定された場合の対応
相関行列表を作成し、相関の高い変数のどちらか一方を取り除いてから再度解析を行います。
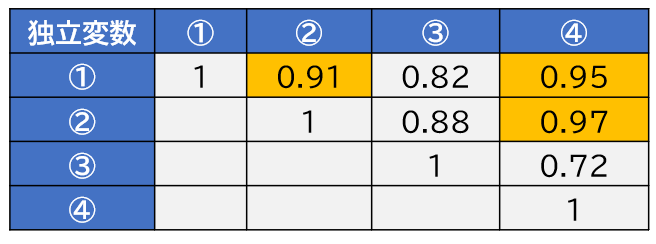
例えば、r≧0.9が3つ（変数①②④）存在する場合はこれらの3つの変数からどれか1つを選んで使用する必要があります。
統計的な変数の選択（変数選択法）
ここまで「仮説による独立変数の選択」「多重共線性を考慮した独立変数の選択」を行いました。最後は、「統計的に有意な変数の選択」について解説します。
統計的な変数の選択とは？
- 解析結果が有意（p<0.05）な独立変数を選択する方法。
- 変数選択法。
変数選択法には以下のような方法がありますが、最も効率が良いのがStepwise法であり、おすすめです。
すべての独立変数を投入する
新たな変数を追加していく
既存の変数を減少させていく
1つずつ独立変数を入れたり抜いたりしながら最適なモデルを探索する
Stepwise法がソフトにあれば、Stepwise法が推奨されているよ！でも多重ロジスティック回帰分析の場合、Stepwise法は統計ソフトによっては使用できないソフトもあるよ
必要な変数は強制投入しよう
変数選択法だけで独立変数を決定してしまうと、臨床的に意味のある変数が抜けてしまうことがあります。臨床経験の基、従属変数に影響を与えると思われる変数は強制投入しましょう。
尤度比による選択法・Wald検定による選択法
- 統計ソフトによっては、尤度比による選択法（変数増加法・変数減少法）、Wald検定による選択法（変数増加法・変数減少法）がある。
- 尤度比による選択法を適用するのがおすすめ。
- 尤度比による選択法では変数増加法と変数減少法で選択される独立変数が異なるので、尤度比の小さいほうの結果を採用する。
②多重ロジスティック回帰分析にて解析
従属変数が2群の差・独立変数が2つ以上であることを確認して、多重ロジスティック回帰分析を適用する。
③多重ロジスティック回帰分析の解析結果を確認
多重ロジスティック回帰分析後は「モデルχ²検定（尤度比検定）の結果」「各変数のオッズ比」「Hosmer－Lemeshow検定の結果」を確認します。ここに記載の検定の結果は、論文を記載する際に全て記載するようにしましょう。
特にモデルχ²検定（尤度比検定）の結果は必須だよ。
モデルχ²検定（尤度比検定）の結果を確認
まず最初にモデルχ²検定（尤度比検定）がp<0.05であるかを確認します。
モデルχ²検定（尤度比検定）とは？
- この検定の結果は、従属変数に対して、独立変数の組み合わせが有意に影響するかどうかを示す。
- この結果が役に立つか立たないかを示すため、必ず結果を記載する必要がある。
もしこの結果がp>0.05であれば、この結果は役に立たないので解析は終了となります。
各変数のオッズ比を確認
モデルχ²検定（尤度比検定）の結果が有意であれば、次に進みましょう。
オッズ比については上記解説を参照してください。また詳しい解説は下記の記事を参照してください。
モデルχ²検定（尤度比検定）の結果が優先されるから、オッズ比がp≧0.05でも気にしないで大丈夫です。ちなみに定数項の結果は無視して大丈夫だよ。
Hosmer－Lemeshow検定の結果を確認
Hosmer－Lemeshow検定とは？
- 回帰式の適合性（当てはまりのよさ）を分析する検定であり実測値と予測値を比較する
- 重回帰分析における決定係数R²（予測精度）のようなもの
- P≧0.05の時に、回帰式が良く適合していると判断する
多重ロジスティック回帰分析でもR²などが算出されるけど、多重ロジスティック回帰分析の場合はHosmer－Lemeshow検定の結果を示すことが推奨されているよ。
「判別的中率の確認」
判別的中率とは？
- 全ての観測値数のうちで観測した値と、予測した結果が一致した割合のこと
- つまり予測の精度のこと
- 80％以上であれば概ね予測精度は良好であると考える
モデルχ²検定はモデルが役に立つかを確認し、Hosmer－Lemeshow検定と判別的中率は適合度の基準、つまり予測精度を表すよ。
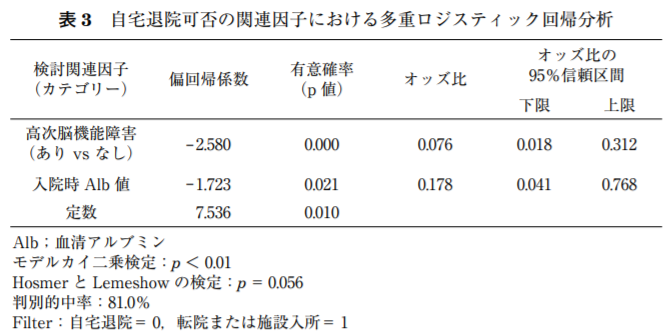
実際の論文では？
これは理学療法士さんの論文で、急性期脳梗塞の患者さんの自宅退院可能かどうかの関連因子を調査した研究です。
自宅退院の可否を従属変数、性別やアルブミンの値、NIHSSなどを独立変数として使用しています。
分析方法
変数の選択方法
この研究では下記の手順で変数を選択しています。
- 文献検討により選択した変数でデータ収集
- 量的変数は2標本の検定（自宅退院群と転院群）、質的変数は分割表の検定を行い有意差のあるものを独立変数に選択。これは統計的に有意な変数を選択しているので変数選択法と同じ考え方です。
- 多重共線性を考慮して相関係数による変数の選択
- 臨床的に意味のある変数の選択
多重ロジスティック回帰分析の結果の解釈
- モデルχ²検定の結果はp<0.01、Hosmer－Lemeshow検定の結果はp=0.056で問題なさそうです。
- 判別的中率は81％で良好な予測精度です。
- Albのオッズ比を見ると、0.178。つまり、Albが1上昇すると、自宅→転院が0.178倍になる。オッズ比が1以下の時は逆数で考えると分かりやすい。逆数は5.62であり、Albが1上昇すると転院→自宅が5.62倍。自宅退院にはAlbが大きく関係していそうですね。
カットオフ値を検討する意義
- カットオフ値とは、陽性・陰性などの判断基準となる値のことです。
- ROC曲線はカットオフ値を検討する際に参考する図です。
- 多重ロジスティック分析では従属変数があり・なしなどの２つの属性なので、カットオフ値を求めることが良くあります。
- 看護の研究では、転倒の要因を検討して転倒のある・なしのカットオフ値を検討するなどです。
カットオフ値まで求めると、直接実践に繋がる研究になりそうだね。
まとめ
多重ロジスティック回帰分析は、難しそうなイメージがありますが、覚えてしまえばとても便利な解析方法です。
覚えるべき点を以下の３つにまとめました。
- 独立変数を選択する方法を理解する
- 解析結果で確認するポイントを理解する
- オッズ比を正しく解釈する
ポイントだけ理解して、早速使ってみよう。実践あるのみ！
この記事を読んだ方におすすめの書籍を下記で紹介しています。良かったら参照してください。
研究では統計解析のために膨大なデータ（アンケート調査のデータなど）を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも１つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!（エミーオ）がおすすめ！で紹介しているので良かったら参照してください。
引用・参考文献
- 対馬栄輝(2020).医療統計解析使いこなし実践ガイド.羊土社,東京.
- 対馬栄輝（2019）.医療系研究論文の読み方・まとめ方.東京図書,東京.
コメント