Last Updated on 2023年12月28日 by カメさん

こんにちは!看護師のカメさん(@49_kame)です。
この記事は10分程度で読めます。

今回はサンプルサイズ(対象者数)の設定方法について解説するよ。
サンプルサイズの設定根拠を明確にすることは科学的水準(研究の質)を担保するために重要です。研究計画書を記載する段階から、サンプルサイズを入念に検討しましょう。
研究計画書の書き方は下記で詳しくまとめています。興味のある方は参照してください。
【研究計画書の書き方】看護師必見「研究計画書・依頼文書(承諾書)・説明文書・同意書(同意撤回書)のフォーマットもあるよ」

サンプルサイズはクリティークをする際にも重要なポイントになるよ。クリティークについて詳しく知りたい人は下記を参照してね。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。
サンプルサイズを設定する方法
サンプルサイズを設定する方法には大きく分けて下記の2つの方法があります。
➀検定力分析(power analysis)によって算出する方法
「➀検定力分析によって算出する方法」は、統計の結果が「有意水準(α)」、「検定力(1-β)」、「サンプルサイズ」、「効果量」の4つの要素の関連性から生じることに基づいた算出方法です。
「②区間推定に基づいて算出する方法」とは、統計により推定したい母数の95 % 信頼区間の幅を事前に設定することにより算出する方法です。
サンプルサイズは大きければ良いの?
統計では、サンプルサイズが大きくなるとp値が小さくなる特性があります。サンプルサイズが大きい方が、同じ相関係数や平均の差であっても有意確率は小さくなります。

ほんとは有意な差がないような結果でも、サンプルサイズを大きくすると意味のある結果に見えちゃうね。また、サンプルサイズを大きくすると言うことは研究の負担が増大するよ。
このような問題点を防ぐためにもサンプルサイズの設定が重要です。またp値だけではなく複数の推測統計指標(信頼区間や効果量など)を用いて評価を行うことも有用とされます。
➀検定力分析(power analysis)によって算出する方法
まずは検定力分析にてサンプルサイズを算出する必要性を解説した後に、具体的な方法を解説します。
なんで検定力分析でサンプルサイズを算出するの?
前述の通り、統計では「有意水準(α)」、「検定力(1-β)」、「サンプルサイズ」、「効果量」の 4 つの要素により検定結果の精度が決まります。また、これら 4 つの要素は、他の3つが決まると残りの1つも決まるという特性があります。

検定力とは「正しく帰無仮説を棄却できる確率」のこと。簡単に言うと、差があるものを正しく差があると言える確率のことだね。
「効果量」「検定力やαエラーβエラー」については下記の記事でまとめているので参照してください。
【効果量とは?】看護師必見「効果量の種類や、効果の大きさの目安も解説するよ」
【αエラー・βエラーとは?】第1種の過誤(αエラー)と第2種の過誤(βエラー)、検出力(1-β)について分かりやすく解説!
検定力(1-β) は 0.8が推奨されています。また有意水準(α)は 0.05と決まっていることが多いです。そのため、研究計画で重要になるのが「効果量」と「サンプルサイズ」の設定です。
サンプルサイズの設定では、ちょうど良いサンプルサイズを設定することが重要です。
前述の通り、サンプルサイズが大きすぎると差が無いのに「有意差あり」としてしまう可能性があります(検定力が大きすぎる)。またサンプルサイズが小さくても問題があり、サンプルサイズが小さすぎると差があるのに「有意差なし」としてしまう可能性があります(検定力が小さい)。
ちょうど良いサンプルサイズを設定するために有用なのが検定力分析を用いた算出方法です。

できるだけ小さなサンプルサイズで、検定力を大きくすることが理想だね。小さなサンプルから母集団の特性を推測するのが統計の目的であることを忘れないようにしよう。
効果量とは?
効果量とは実質的な差を表す指標です。p値は差があるか無いかの確率は分かりますが、実質的な差の大きさは分かりません。また前述のようにサンプルサイズに影響される特性もあります。そのため、サンプルサイズにも影響されない標準化された差を表す指標である「効果量」が便利です。
効果量については下記の記事で詳しく解説しています。良かったら参照してください。(現在作成中)
検定力分析の具体的な方法
検定力分析(power analysis)には2つの目的があります。

②は帰無仮説が棄却されなかったとき、つまり「差がない」て結果だった時に、改めて確認することが多いよ。
①②どちらの計算も、「4 つの要素のうち、他の3つが決まると残りの1つも決まる」という検定力分析の特性を利用します。
①事前にサンプルサイズを決める検定力分析
この分析は研究の計画段階で行います。
サンプルサイズは先行研究から推測される「効果量」「有意水準(α)」「検定力(1-β)」からサンプルサイズを算出します。
検定力分析の計算は下記に記載のG*Powerを使用して行うことが多いです。
②事後に検定力を調べる検定力分析
研究にてデータ収集を行った後に行います。
「サンプル・サイズ」「効果量」「有意水準(α)」から「検定力(1-β)」を算出します。
①と同様に検定力分析の計算は下記に記載のG*Powerを使用して行うことが多いです。
G*Powerを使用した検定力分析
検定力分析はWeb上で入手できるフリーソフトG*Powerを使用することが多いです。そのためG*Powerを使用した検定力分析の方法を簡単に解説します。

G*PowerはMacでもWindowsでも使えるよ。
G*Powerのダウンロード方法
G*Powerは、ハインリッヒ・ハイネ大学デュッセルドルフ校の実験心理学研究所のホームページ
よりダウンロードすることができます。
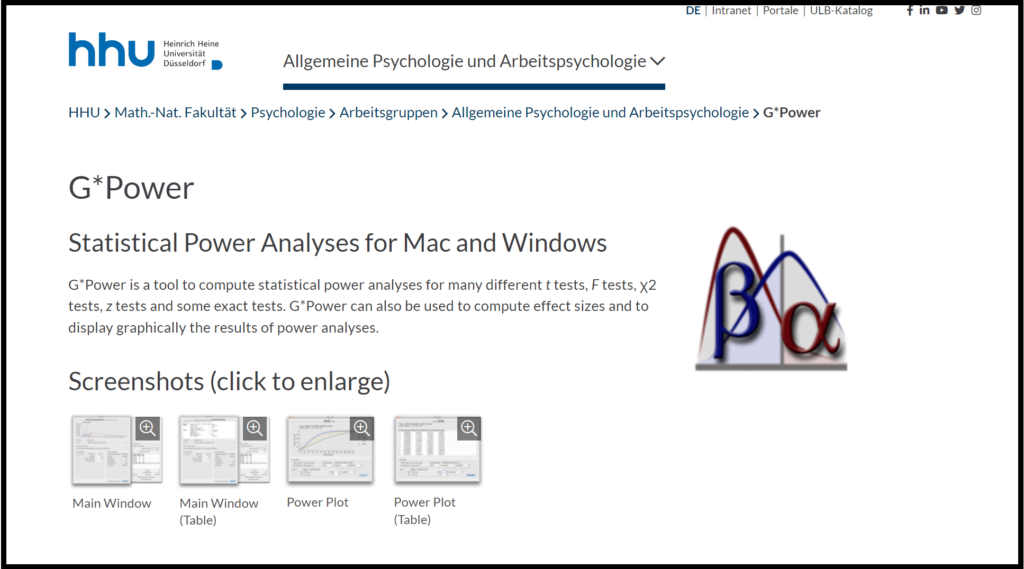
ページ中部からWindows XP/Vista版もしくはMac OS 7-9版をダウンロードすることができます。
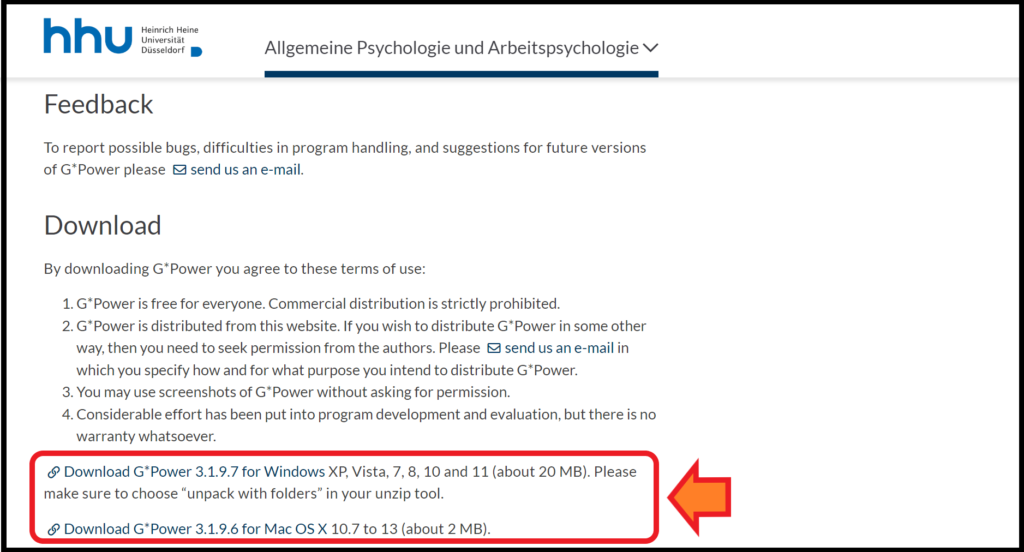
ダウンロードしてファイル内の「setup」よりインストールを行います。
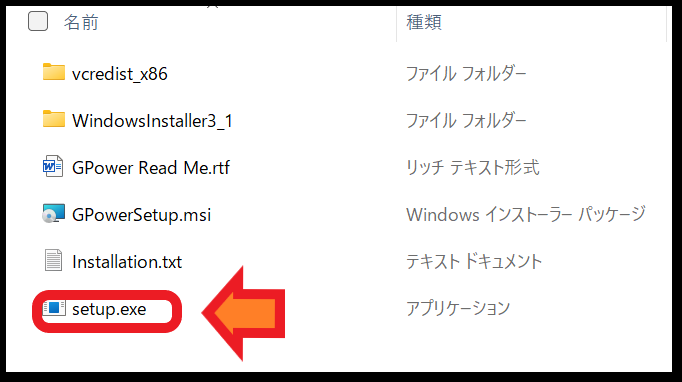
案内に従ってインストールしましょう。Nextをクリックしていけばインストールできます。

下記がG*Powerの操作画面です。
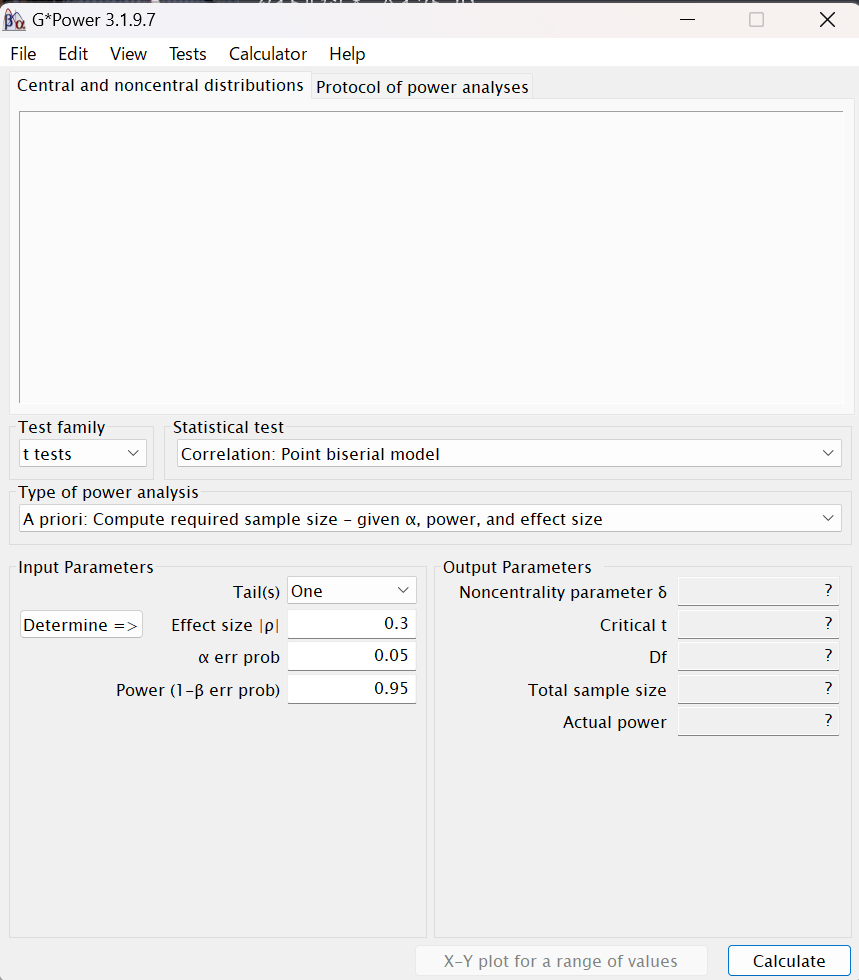
G*Powerを使用した検定力分析の例
今回は「対応のないt検定」を行う際の検定力分析(サンプルサイズを決める or 検定力を調べる)について例を示します。
Test familyは「t tests」と選択します。

Statistical test Meansには「Means:Difference between two independent means (two groups)」を選択します。
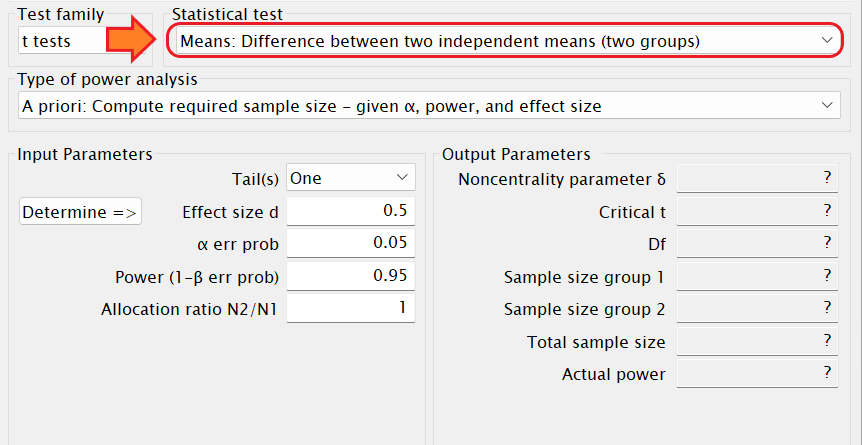
Type of power analysisには、
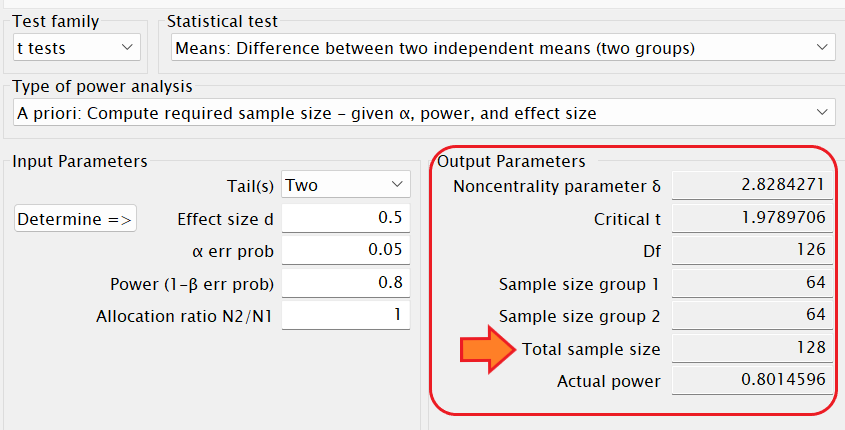
事前のサンプルサイズの算出の場合は「A priori: Compute required sample size – given α, power, and effect size」を選択します。
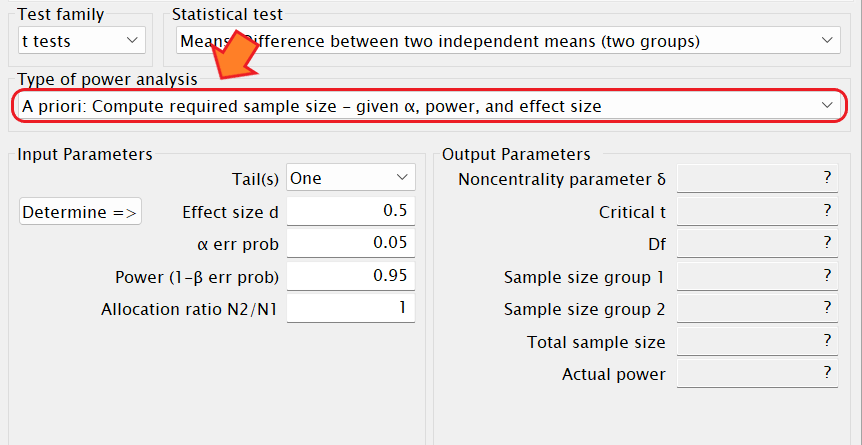
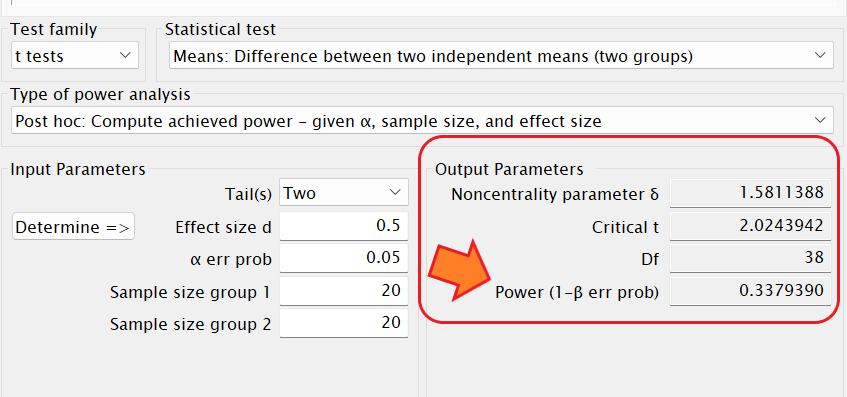
事後の検定力分析の場合は「 Post hoc: Compute achieved power – given α, sample size, and effect size」を選択します。

Input parametersには、
事前のサンプルサイズの算出の場合はTails(s)は「Two」を選択します。
Effect size dには、先行研究からわかっている効果量の大きさ、もしくはを今回の研究で予測される効果量:d = 0.2(効果量小)、0.5(効果量中)、0.8(効果量大)を入力します。

何もわからなかったら0.5(効果量中)を入力しよう。
α error probは有意水準のことです。0.05と入力しましょう。
Power (1–β error prob)は検定力です。0.8と入力しましょう。
Allocation ratio N2/N1は2 つのグループの n数の比を入力します。例えばn1=10人、n2=10人の場合は比は「1」、n1=20人、n2=10人ならば「0.5」を入力します。
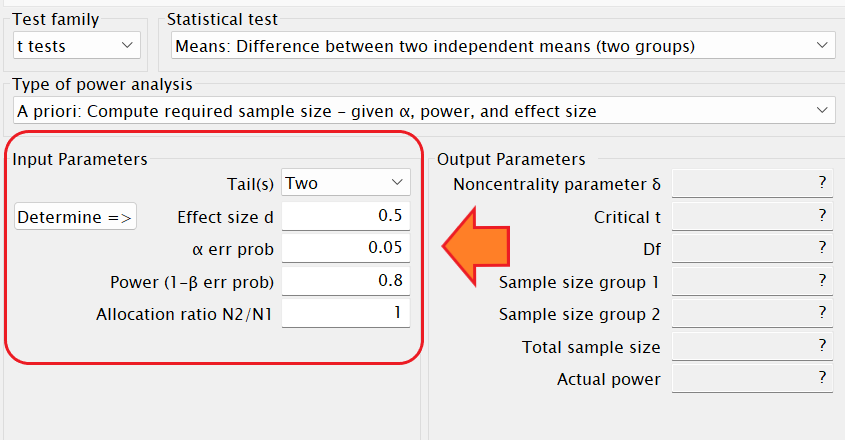

「サンプルサイズ」を算出する場合は、他の3つ要素「効果量」「有意水準(α)」「検定力(1-β)」を使用した計算になるよ。
上記を入力して「Calculate」をクリックすると、必要サンプルサイズが算出されます。
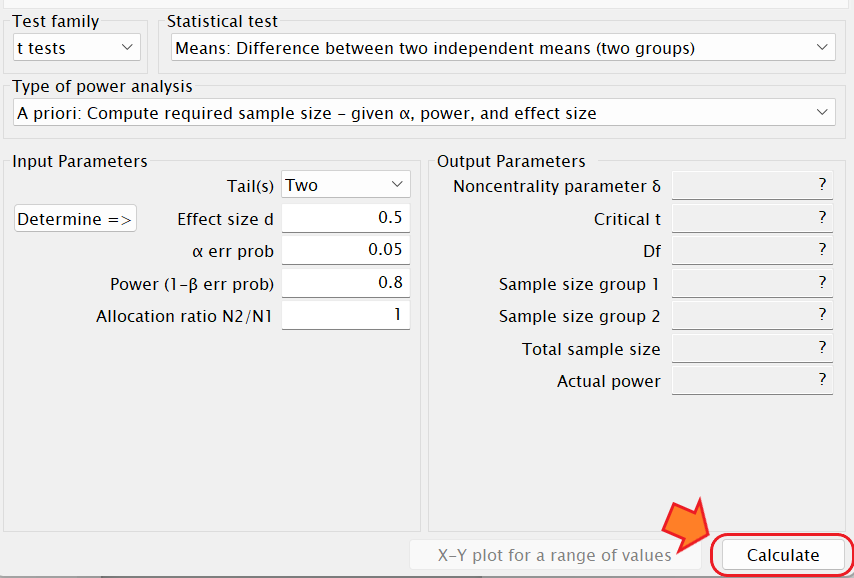
事後の検定力分析の場合のInput parametersは、
Tails(s)は「Two」を選択します。
Effect size dは研究で得られたデータの効果量を入力します。
α error probは有意水準なので0.05を入力します
Sample size group 1はグループ 1のサンプルサイズ(n数)を入力します。
Sample size group 2はグループ 2のサンプルサイズ(n数)を入力します。

上記を入力して「Calculate」をクリックすると、今回の研究による検定力が算出されます。

「検定力(1-β)」を分析する場合は、他の3つ要素「効果量」「有意水準(α)」を使用した計算になるね。
効果量も計算できる
Determineをクリックすると、各グループのMean や SD を入力してCalculateをクリックすることで効果量を計算することができます。
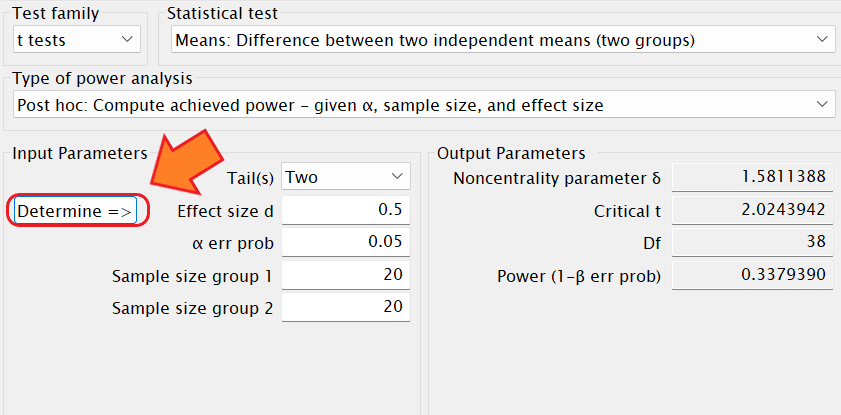
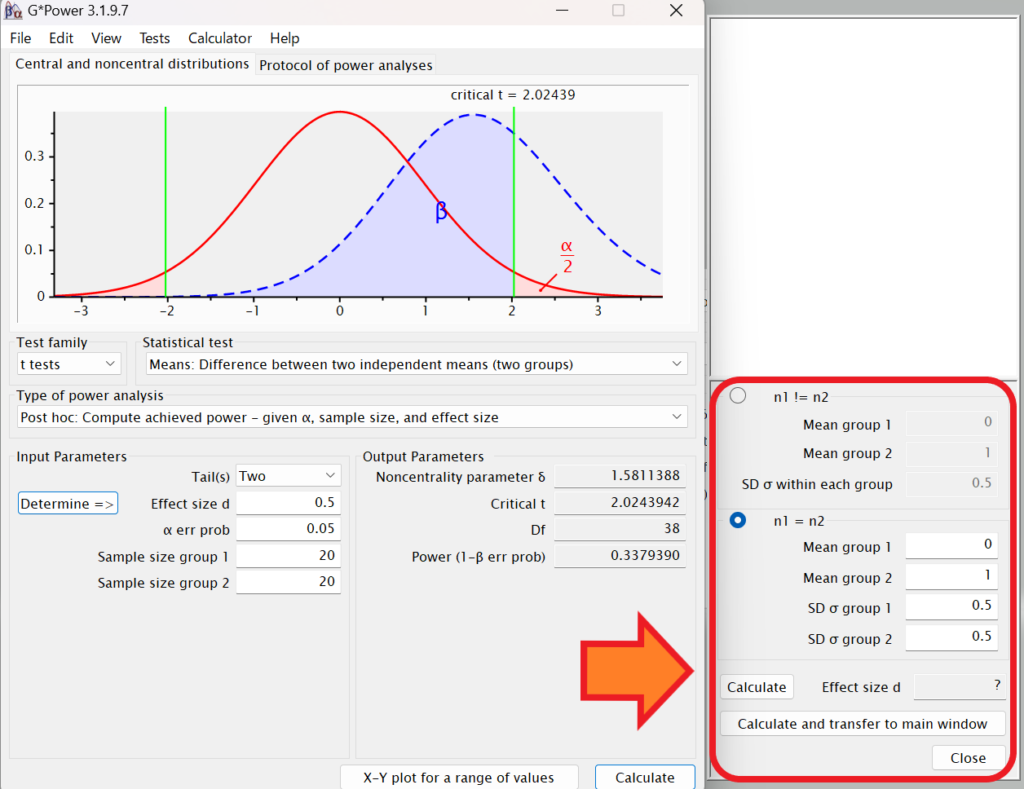
n1=n2をクリックします。
Mean group1とMean group2にはグループ1とグループ2の平均値をそれぞれ入力します。
SD σ group1とSD σ group2にはグループ1とグループ2の標準偏差をそれぞれ入力します。
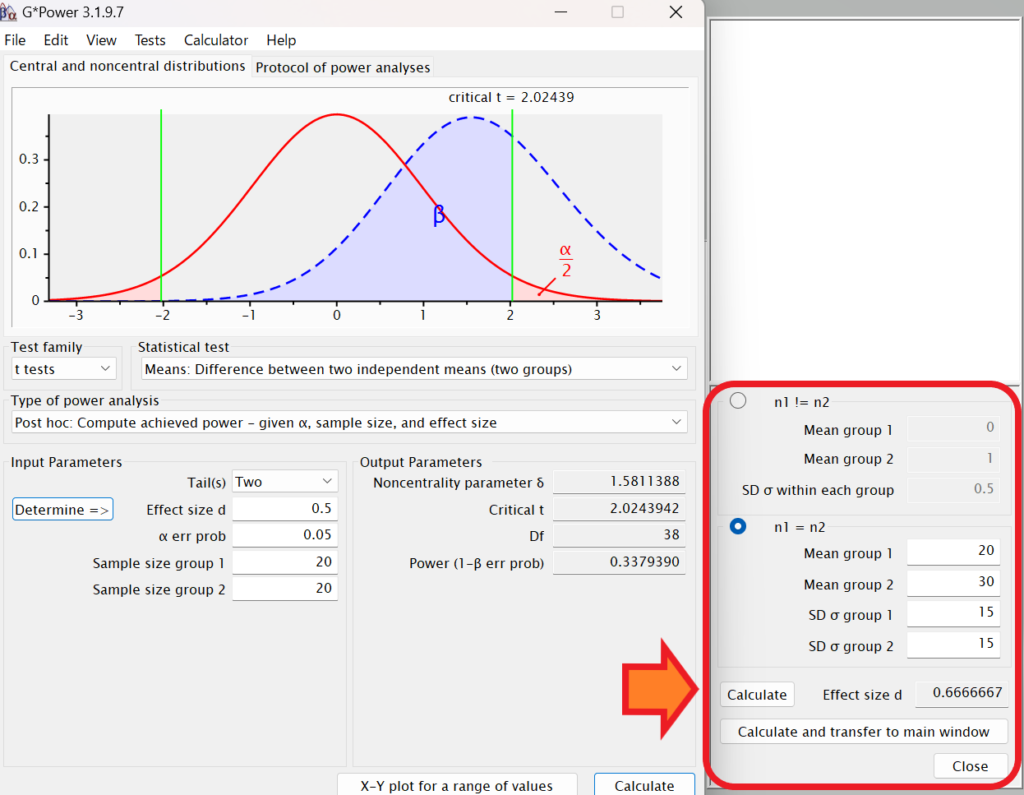
例えば、Mean group1:20、Mean group2:30、SD σ group1:15、SD σ group2:15と仮定して「Calculate」をクリックすると効果量が0.6666667と算出されます。

他の分析方法に関する検定力分析の例は下記の文献を参照してね。
chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://www.mizumot.com/method/mizumoto-takeuchi.pdf
②区間推定に基づいて算出する方法
サンプルサイズの算出には前述の検定力分析の他に、区間推定を用いて算出する方法があります。
区間推定を用いてサンプルサイズを算出する際は、「信頼区間」と「標準誤差」を理解することが重要です。
信頼区間とは?
区間推定とは、母集団が正規分布に従うと仮定できる場合に、実際に収集した標本のデータを用いて母平均を区間(幅)で推定することです。

一つの数字で推定するのではなくて、一定の幅で推定することだね。
そして推定する区間が「信頼区間(confidence interval:CI)」と呼ばれます。
例えば「母平均の95%信頼区間」を求める場合、母集団から標本のデータを取り出し、その標本から母平均を求めることを100回実施すると、その区間(100個の信頼区間)に95回は母平均が入るということです。
信頼区間は幅が狭い程、精度が高く利用価値が高いと言われています。また信頼区間の幅はサンプルサイズが大きくなると狭くなります。
「信頼区間」や「母集団と標本」については、下記の記事で詳しくまとめています。興味のある方は参照してください。
標準誤差とは?
また、区間推定からサンプルサイズを算出する際に必要になるのが「標準誤差(standard error:SE)」です。標準誤差とは「標本平均」が「母平均」に対してどのくらいばらついているのかの程度を表す指標です。つまり統計で推定した結果が本当の値からどのくらい離れているかの幅を示す値です。
標本調査(統計の検定)では、「標本平均(推測した値)の前後に標準誤差の1.96倍の幅をとると、母平均(真の値)がその中に入る確率は95%である」と言えます。ちょっと難しいですが、これを示したのが下記の図です。
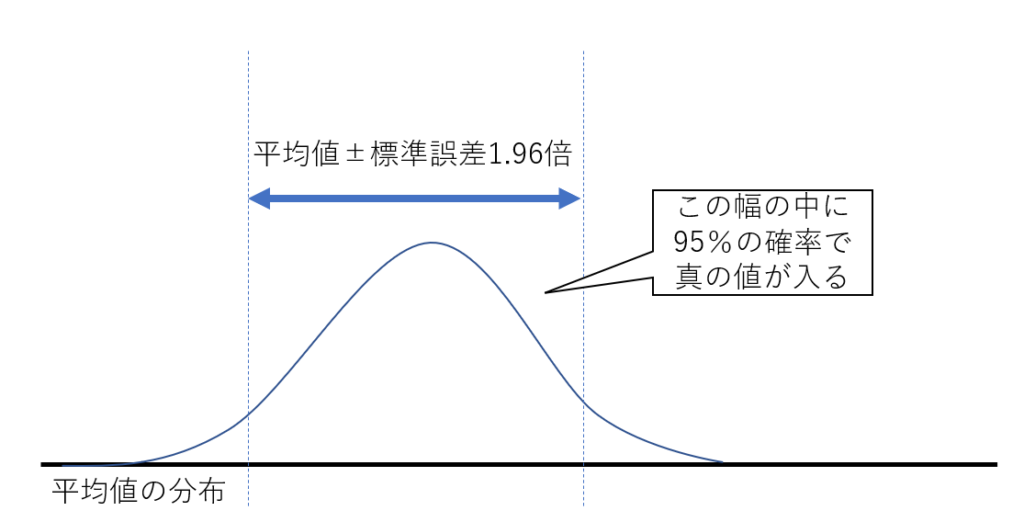
平均値±標準誤差の1.96倍の幅の中に95%の確率で真の値が入ります。ちなみに平均値±2倍の幅の中には95.5%の確率で真の値が入ります。

この範囲が前述の信頼区間で、この区間に入る確率が信頼係数だよ
標準誤差の値が小さいということは、小さい幅(精度が高い)の中に真の値が入っているということであり、逆に標準誤差の値が大きいということは、大きな幅の中に真の値があると推測されるということになります。
サンプルサイズが大きいほど標準誤差は小さく(信頼区間の幅が狭い)なります。サンプルサイズが大きいと信頼区間が狭くなり推定の精度が高くなります。

統計の目的は、少ない標本から母集団の特性を推定すること。できるだけ正しい母集団の平均を予想したいから標準誤差は小さいことが理想だね
標本誤差と標準誤差の違い
標本誤差とは母集団と標本の値の差のことであり、
標準誤差とは標本分布のばらつきのことです。
つまり、標本誤差を確率で考えて、誤差のばらつきを示したのが標準誤差です。
サンプルサイズは大きければ良いの?
サンプルサイズが大きくなれば、「標準誤差」は小さくなります。そして信頼区間も狭まります。結果として推定の精度も高まります。
しかし、統計の性質上、サンプルサイズが大きいほど有意になりやすいという特徴があることから、サンプルサイズが大きいと、ノイズレベルの差や効果を有意な結果としてしまう可能性があります。
また、研究の実現可能性としても大きすぎるサンプルサイズは理想的ではありません。事前に研究者が、信頼区間の幅をどの程度にするのかを設定し、その上でどの程度のサンプルサイズが必要なのかを計算していくことが重要です。
区間推定からサンプルサイズを算出するための要素
区間推定からサンプルサイズを算出する際は、下記の項目を設定する必要があります。
➀母集団の規模
母集団の規模とは、統計にて推定しようとしている母集団の大まかな人数です。
例えば、全国の看護師を母集団とするならばー人くらいですし、ある県の看護師だったらー名程度、A大学病院の看護師だったら500名程度などです。自分の研究で標的とする母集団の人数を考えましょう。
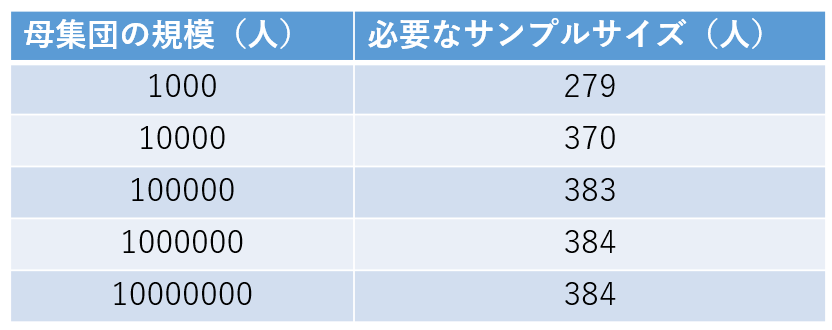
母集団が1万人以上は、必要なサンプルサイズはほとんど変わりません。
「許容誤差±5%,信頼レベル95%、回答比率50%」に設定すると、母集団が1万人以上の場合に必要なサンプルサイズは380人程度です。
②標準誤差(許容誤差)
サンプルサイズの計算では、許容誤差という言葉が使われますが、考え方は前述の標準誤差と同様です。つまり、標本調査により得られた結果が、母集団の結果かどの程度離れている可能性があるかを表す指標です。
調査結果には必ず誤差が生まれます。その誤差をどの程度許容するのかを事前に設定します。

これは調査の正確性に直結するね。
一般的に許容誤差は±1~10%で設定します。標本調査で得られた数字と、母集団の数字が±1~10%の範囲でズレる可能性があるということです。
③信頼度(信頼係数)
標本調査により得られたデータが、どのくらいの確率で許容誤差内に収まるかを表す指標です。
信頼度95%とは、100個のデータのうち、95個のデータが許容誤差内に収まる状態です。
許容誤差も信頼度も高い方が望ましいです。しかし許容誤差の範囲を狭めて、許容誤差の中に沢山のデータを収めようとすると膨大なサンプル数が必要となります。

研究の実現可能性にも関わるポイントだね。後。統計の基本的な考えである、「できるだけ少ない標本で」というのを忘れないようにね。
信頼度は一般的に90〜99%に設定することが多いです。現実的なサンプルサイズを考えると、信頼度95%に設定することをおすすめします。
④回答比率
回答比率とは、「該当の回答を選ぶ割合はどの程度か?」ということです。つまり、「はい」と「いいえ」のうち「はい」を選ぶ割合はどの程度かということです。
しかしこれを調査するのが研究の目的なので、事前に分からないことがほとんどです(先行研究で同じ質問の調査をしている場合は参考にできますが…)
そのため、一般的には0.5(回答比率50%)と設定します。なぜかというと、回答比率を50%に設定すると、誤差が最大になり必要なサンプルサイズも最大になるからです。

分からない時は多めにデータ取るしかないからね
区間推定からサンプルサイズを算出する具体的な計算方法
それでは具体的な計算方法を解説します。
Web上には自動計算フォームを使っても良いですが、研究計画書や論文を記載する際に困るので、できるだけ自分で計算しましょう。

計算が苦手な人のためにExcelの計算フォームも作ったから活用してね。
区間推定からサンプルサイズを算出する計算式は以下の通りです。
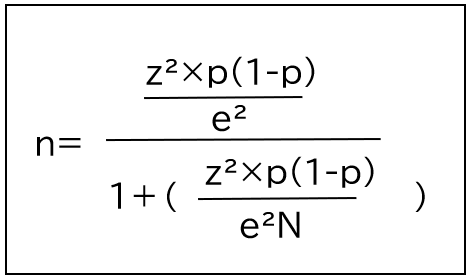
n=必要なサンプルサイズ (人)
N=母集団の規模 (人)
z=信頼度(小数点表記)
p=回答比率 (小数点表記)
e=許容誤差 (小数点表記)
ちなみに母集団の規模を加味しない計算式は以下になります。
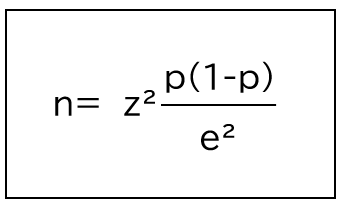
上記と同様の例で許容誤差:±5%(0.05)で、信頼度:95%(1.96)、回答比率:50%(0.5)で計算すると必要なサンプル数は、約384となります。
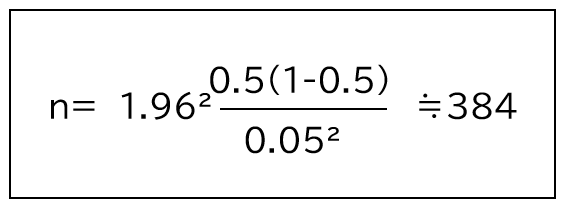
母集団の規模を加味しても加味しなくても大きな違いはありません。
電卓で計算するのが苦手な人はExcelの計算フォームを作成したので使ってみてください。
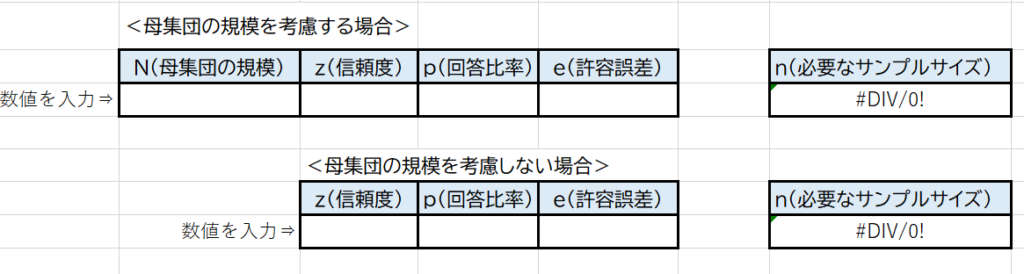

研究計画書や論文に記載する際は、「母集団の規模を○○名、信頼度を95%、許容誤差を5%、回答比率を50%と設定して算出(Microsoft® Excel® 2019 MSO バージョン 2111)した」等の記載すると良いよ。
信頼度を計算式に入力する時の注意点
信頼係数が90%であれば「1.64」
信頼係数が95%であれば「1.96」
信頼係数が99%であれば「2.58」
を入力してください。
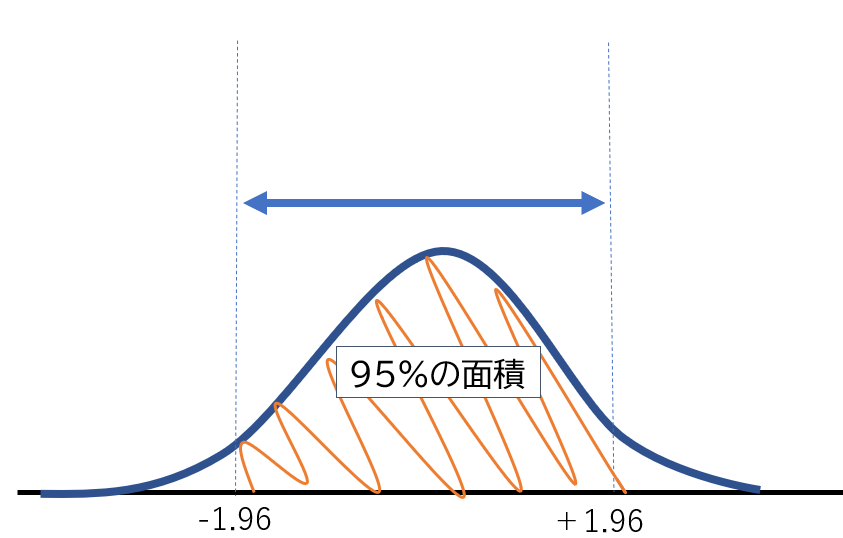
これらの数字の意味は下記の正規分布の図で、例えば中心0から±1.96の範囲が95%の面積になるということです。そのため、信頼係数99%であれば「2.58」という大きな値になっています。
早見表も有用
具体的な数字は知ることはできませんが、大まかにサンプルサイズを把握したい時には「早見表」も便利です。
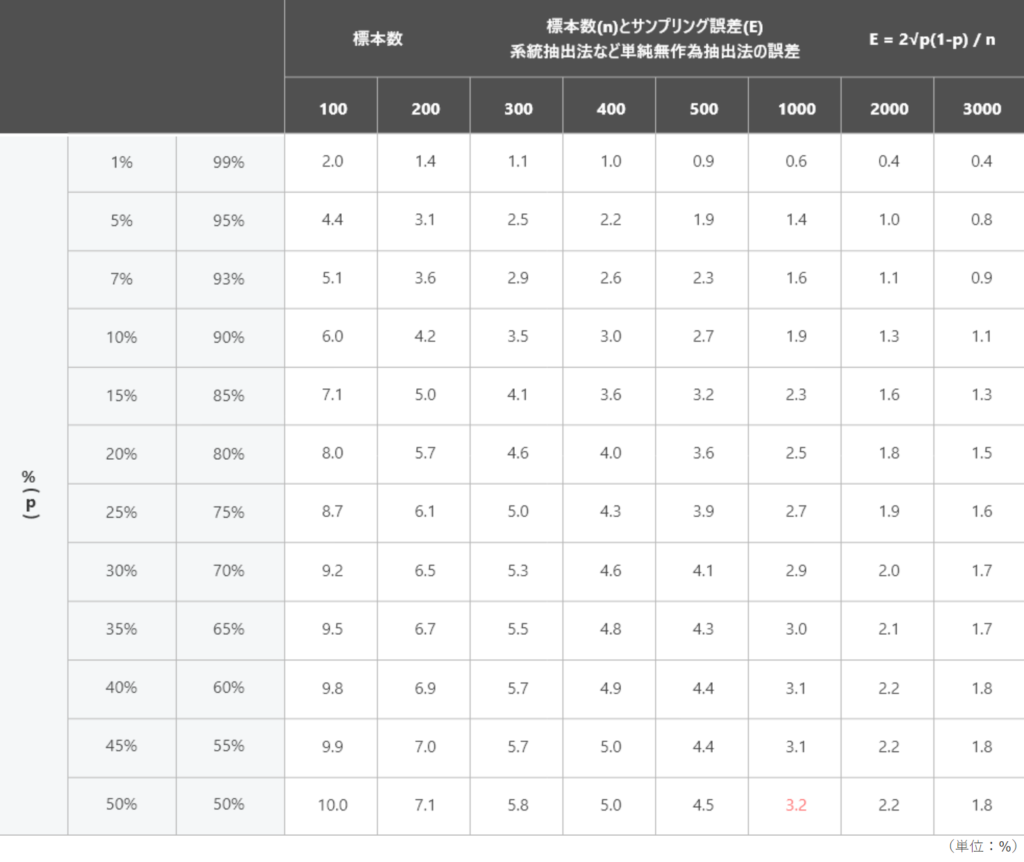
引用:https://www.nttcoms.com/service/research/sampling/

研究の構想を練るぐらいの計画段階とかだね
縦軸の「回答比率」と、表の中の「許容誤差」から、横軸の「サンプルサイズ」を求めます。
例えば回答比率(縦軸)が50%で、許容誤差(表の中)が5%だとすると、サンプルサイズ(横軸)は400になります。上記の計算式で出した数と大きな差がないことが分かります。
多変量解析のサンプルサイズ
ここでは多変量解析を行う際のサンプルサイズの計算について解説します。多変量解析では、多くの変数を扱うため推定する母数も大きくなります。このような特性を考慮したサンプルサイズの設計が必要です。
例えば多重ロジスティック回帰分析の場合は、1独立変数あたりに少なくとも10の標本が必要とされます(独立変数の数×10)。
また重回帰分析の場合は、1独立変数あたりに少なくとも10〜20の標本が必要とされます(独立変数の数×10-20)。
回帰分析において「決定係数」を検定する際には「50+独立変数の数×8」、「回帰係数」を検定する際には「104+独立変数の数」という式も提唱されています(Green 1991 ; Tabachnick et al 2007)
決定係数とは、説明変数が目的変数をどれくらい説明しているか、つまり予測式(回帰式)の精度を表す値です。また回帰係数とは、y=ax+bのa(傾き)のことです。独立変数の影響力を確認する際に使用します(通常は標準化した標準偏回帰係数を使用)。

決定係数も回帰係数もどちらも検定する場合が多いから、その場合は、どちらか大きい方を採用するよ。
多変量解析においても検定力分析が重要
上記の独立変数×10という方法は簡易的で有用ですが、可能であれば前述の検定力分析を行うことが推奨されています。
構造方程式モデリングを行う場合
構造方程式モデリングの場合は、Westland JC.(2010). Lower bounds on sample size in structural equation modeling. Electron Com-mer Res Appl, 9, 476-487.の基準に基づいてサンプルサイズを計算をすることがおすすめです。
下記のサイトで計算できます。
「A-priori Sample Size Calculator for Structural Equation Models」

このサイトであれば根拠も明確だから論文にも記載できるよ。
重回帰分析や多重ロジスティック回帰分析について詳しく知りたい方は下記の記事を参照してください。
質的研究のサンプルサイズ
質的研究におけるサンプルサイズについても考えてみましょう。まず大前提として、質的研究も量的研究も一般性のある結果を発見することが目的です。
その上で、量的研究では個別のデータの偏りを一般性として間違えないように十分な標本数を確保します。しかし、質的研究場合は個別のデータを深く掘り下げることにより一般性のある知見を発見しようという考え方です。
そのため、対象者が1名であっても質的研究は成り立ちます。

量的研究も質的研究も目的は同じだけど、基本的な考え方が違うんだね。
Glove(2015)は、質的研究におけるサンプルサイズは、研究の目的を達成するために量的にも内容的にも十分なデータが得られる対象者数が望ましいとしています。このように質的研究においては事前のサンプルサイズ設定は重要視されていません。
質的研究ではサンプルサイズの量よりも、内容を重要視する
質的研究では便宜的標本抽出法(身近な人に依頼するなど)にてサンプルを設定することがほとんどです。
質的研究においては、研究者の関心がある現象を経験している研究参加者が望ましい(Speziale et al,2007)とされており、抽出するサンプルの基準(適格基準・除外基準)を明確にすることが必要となります。

質的研究ではサンプルの量より質を大事にしよう
注意:算出したサンプルサイズ以上のデータ収集を計画しよう!
算出したサンプルサイズを基に実際の対象者数を設定する方法を解説します。実際の対象者数を計画するときは、欠損値やアンケートの回収率を加味する必要があります。
実際に収集する対象者数は下記の式で求めることができます。
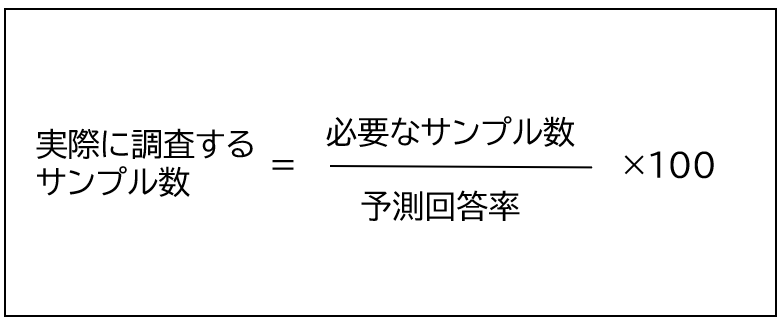
例えば、アンケート調査(Web調査)に必要なサンプルサイズが300名と算出された場合を考えます。
Web調査の回答率は20%とされているため、実際の対象者数は1500名となります。
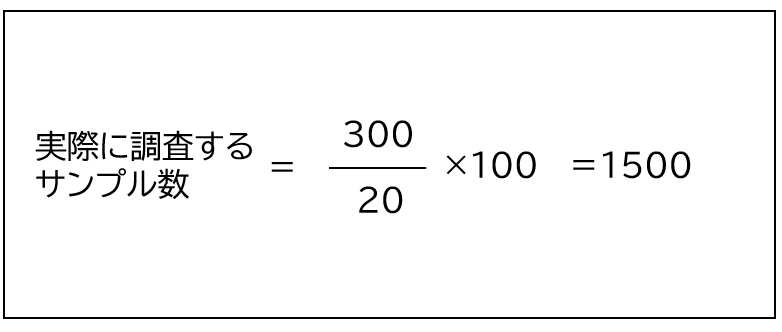

上記の例だと、20%が回答してくれた結果300名のデータが得られるようなサンプルサイズの設計が必要となるよ。
まとめ

サンプルサイズの設定根拠を明確にすることは科学的水準(研究の質)を担保するために重要です。
サンプルサイズが小さければ誤差が大きく、研究の精度が下がります。反対にサンプルサイズ大きくすれば、研究の精度は上がります。しかし、サンプルサイズが大きいと調査にかかる費用や手間が大きくなります。
費用や期間などの実現可能性や、研究の質の担保として、どの程度誤差を許容するかなどを総合的に判断することが必要となります。

少ない標本で結果を推定するのが統計の役割だよ。研究の質を上げるためには、サンプルサイズを大きくするだけじゃなくて、正しい検定方法を活用するのも重要だね。
この記事を読んだ方におすすめの書籍を下記で紹介しています。良かったら参照してください。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。














コメント