Last Updated on 2025年2月17日 by カメさん
こんにちは！看護師のカメさん(@49_kame)です。
今回は３つ以上の対応のあるデータの分析方法について解説します
前編では３つ以上の対応のないデータの分析方法について解説しました。前編について知りたい方は以下を参照してください。
3つ以上の対応のあるデータには反復測定による分散分析を行います。用語が似ていて間違いやすいのでおさらいします。
「新人看護師、2年目看護師、3年目看護師」など異なる3群の比較
「実験前、実験後、実験から一カ月後」などで1つの群から3時点でデータを取る場合
分散分析の前編の記述と重複する部分もあるため、必要ない部分は読み飛ばして分析方法の選択フローを中心に読んでね。
研究では統計解析のために膨大なデータ（アンケート調査のデータなど）を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも１つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!（エミーオ）がおすすめ！で紹介しているので良かったら参照してください。
反復測定による分散分析とは？
反復測定による分散分析とは？
- 3つ以上の群に対して、平均値に差があるかを確認する方法
- 対応のあるデータに使用する
3つ以上の群にt検定は使えない
3つ以上の群に対して、ｔ検定など2つの群の差を分析する検定を繰り返し行うと正しく判定する確率が下がり間違った結果となるため注意しましょう。
多重比較法とは？（前編のおさらい）
多重比較法とは？
- ３つ以上の群のどの組み合わせに平均値の差があるかをを確認する方法
- 有意差は組み合わせ毎に結果が出る
上記の反復測定による分散分析では、3つ以上の群全体として差があるかを確認しました。多重比較法は、更にそれぞれの群間で差があるかを分析したものです。
多重比較法の結果は、A群とB群での有意差とA群とC群での有意差など群毎に結果が出るよ。
分散分析のフロー（前編のおさらい）
分析の流れを以下に示します。
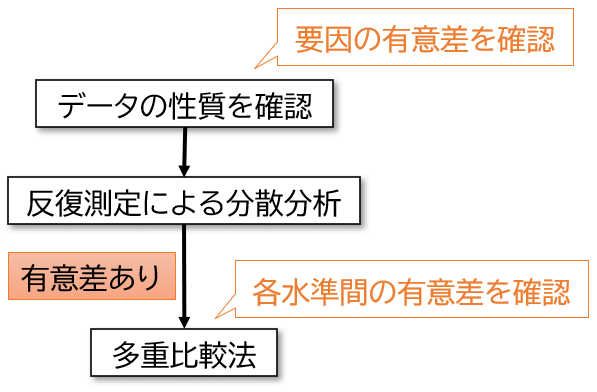
「データの性質を把握して一元配置分散分析を行う。有意な差があれば多重比較法を行う」というのが一般的な流れです。
詳細は下記の「分散分析のフロー」と「多重比較法のフロー」を参照してください。
分散分析が有意でなければ解析終了
分散分析が有意でなく主効果がないのであれば、そこで分析は終了となります。そのため多重比較法の結果を採用することはありません。
分散分析の用語を確認！要因・水準・主効果とは？（前編のおさらい）
要因とは？
要因とは？
- 因子とも呼ばれる
- データの差に影響を及ぼす原因となる変数のこと
年齢で差があるかを調査するならば、要因とは年齢のことです
水準とは？
水準とは？
- 処理とも呼ばれる
- 要因のそれぞれのカテゴリーのこと
要因が年齢であるなら、水準は10代、20代、30代などです。
主効果とは？
主効果とは？
- 要因の平均差のこと
要因を年齢とすると、年齢で有意な差（主効果）を認めた」のように使います。
ちなみに要因で有意な差を認めたならば、多重比較で個々の水準間の有意差を比較するよ。
反復測定による分散分析の、分析方法の選択フロー
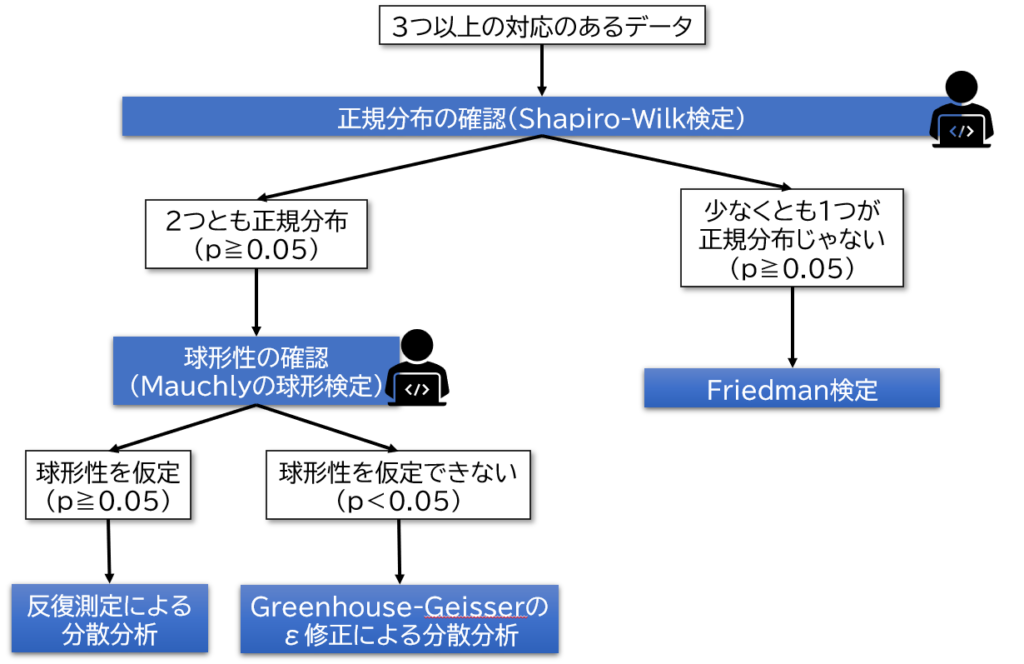
反復測定による分散分析が、一元配置分散分析と異なるところは？
正規性の確認の後で等分散ではなく球形性を確認する
まずはデータの分布を確認し、正規分布かどうかをShapiro-Wilk検定にて確認します。正規分布でなければFriedman検定です。
正規分布であれば、次にMauchlyの球形性検定にて球形性を仮定できるかを確認します。球形性が仮定できれば反復測定による分散分析、球形性が仮定できなければGreenhouse-Geisserのε修正による分散分析となります。
Shapiro-Wilk検定はp≧0.05で正規分布
正規分布や等分散の確認の際は、普段の検定とは異なり、Shapiro-Wilk検定や球形性の検定で「p≧0.05」の場合が「正規分布あり」や「球形性の仮定あり」となるので注意してください。
多重比較法の選択フロー
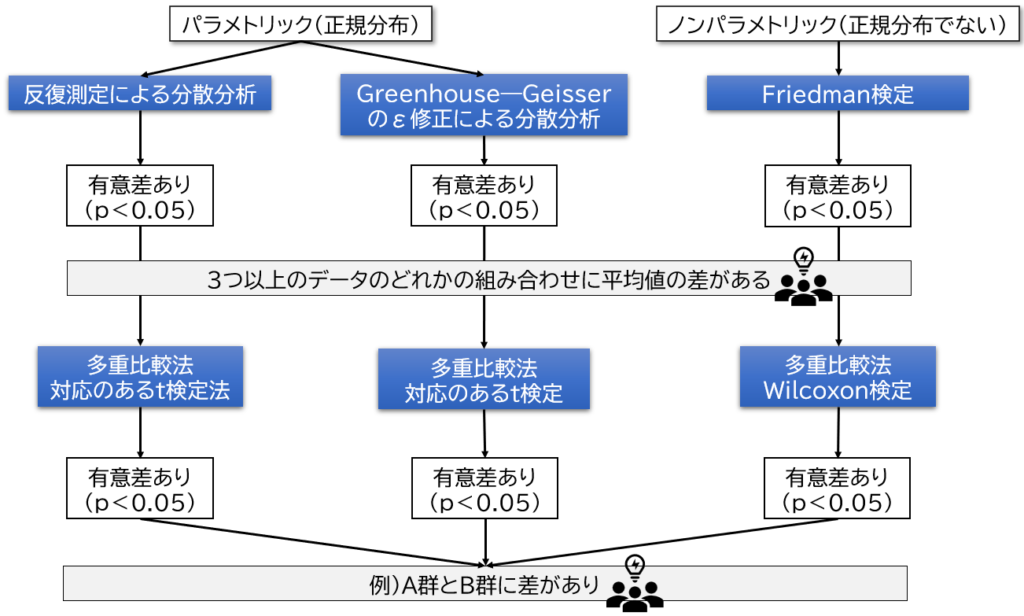
例としてp=0.05を基準としています
上記の分散分析の分析方法の選択の続きです。選択した分散分析の分析方法によって多重比較法が異なります。
分散分析の方法が「反復測定による分散分析」、「Greenhouse-Geisserのε修正による分散分析」、「Friedman検定」のどれかに選択して分析を行います。分散分析で有意差が出なければ解析はそこで終了となります。
もし分散分析で有意差がでれば、多重比較で水準間の有意差を確認しましょう。多重比較法の選択は、「反復測定による分散分析」および「Greenhouse-Geisserのε修正による分散分析」ならば「対応のあるｔ検定」、「Friedman検定」ならば「Wilcoxon検定」を選択して分析します。
対応のあるｔ検定やWilcoxon検定は、2群の検定を行う際に出てきましたね。詳しくは以下の記事を参照してください。
多重比較法で2群の比較を繰り返して大丈夫？
この記事の冒頭で2群の比較を繰り返すと、正確な結果が出ないと説明しました。そのため、上記の多重比較法において「ｔ検定」や「Wilcoxon検定」が出てきて疑問に思われた方もいると思います。
その問題を理解するために登場するのが確率です。
検定を繰り返すほど正しく判定する確率（例えば95％）が低下していきます。そのため、多重比較法での「対応のあるｔ検定」や「Wilcoxon検定」では有意水準を低めに調整しながら解析しています。
有意水準の調整は統計ソフトが計算してくれるから、難しく考えすぎなくて大丈夫だよ。
分散分析・多重比較法の結果の解釈
分散分析・多重比較法で有意な差があったとすると？
「反復測定による分散分析の結果、要因間でp＜0.05で有意な差（主効果）を認めた。多重比較法にてどの水準間に差があるかを比較したところ、AとBの水準間でp<0.05で有意な差を認めた。」
といった結果の読み取り方になります。
分散分析で有意な差があったが、多重比較法で有意な差が無かった場合は？
「反復測定による分散分析の結果、水準間でp＜0.05で有意な差（主効果）を認めたものの、水準間での差は明確とならなかった。」
という結果の解釈になります。
分散分析で有意差がなく多重比較で有意差ありとなった場合は？
「一元配置分散分析の結果p≧0.05で有意な差は認めなかった。」
先の検定である分散分析の結果を採用するため、多重比較法の結果は採用せずに上記のような結果の解釈になります。
結果の解釈のポイント
分散分析の前編でも述べましたが、統計解析結果だけではなく個々のデータにも着目するようにしましょう。
特に反復測定の分散分析の場合は個々のデータの変化を3時点以上で追うような研究が多いため、個々のデータの特性から読み取ることができる情報が沢山あります。
統計解析結果だけじゃなくて、臨床経験を活用して分析してみてね。
反復測定による分散分析の実際の論文
今回紹介する論文は初発の乳がん患者のQOLの変化を経時的に調査した論文です。
対象者のQOL等を術前、術後1週間、術後2週間、術後3カ月、術後1年の5時点で経時的に収集しています。そのデータを反復測定の分散分析にて比較し、さらに多重比較法を使用して比較しています。
データ特性の確認を行っていないので、できれば正規性の確認など、データ特性を見た上で分析方法を選択することができたら良かったですね。
多重比較法ではBonferroni の方法を用いています。この方法は上記では紹介していませんが、これもまた良く使われる多重比較法です。
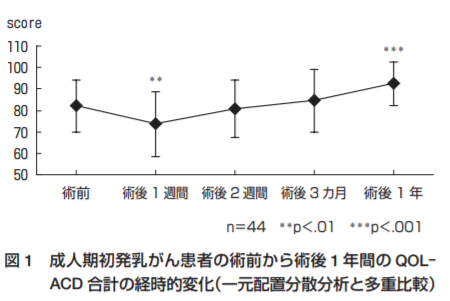
この図はQOLの経時的な変化を図にしたものです。反復測定の分散分析の場合は、数字や有意差の有無だけではなく、このようにグラフを参照しながら臨床的に見て意味のある変化かどうかを検討します。
今回の表で有意差ありの＊がついているのは、おそらく多重比較法で術前と比べて有意差があったのデータだと思います。
今回の論文では、2つの変数についての経時的な調査も行なっています。このような分散分析を二限配置分散分析と言ったりします。その場合は2つの変数による主効果だけでなく、2つの変数による相互作用があるかどうか(交互作用)も確認する必要があります。
まとめ
分散分析による解析方法を選択する際は、扱うデータが対応のない独立したデータなのか対応のあるデータなのかを確認しましょう。またデータが正規分布かどうかによっても分析方法が変わるため、収集したデータの分布も確認するようにしましょう。
分散分析には多重比較法がセットです。2つの解析を行うため結果の解釈を慎重に行うようにしましょう。
この記事を読んだ方におすすめの書籍を下記で紹介しています。良かったら参照してください。
研究では統計解析のために膨大なデータ（アンケート調査のデータなど）を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも１つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!（エミーオ）がおすすめ！で紹介しているので良かったら参照してください。
おまけ
初発の乳がんの方に5時点でこのようなアンケートを取るということが、どのくらい精神的負担になるか分かりませんが、個人的にはアンケート回数が多い印象を受けました。
「研究だから」「先行研究の裏付けがあるから」という理由だけではなく、研究対象者への配慮はどうかという視点も重要だと感じます。
このように考えると、データ収集をした以上は責任を持って研究を続け、成果を出さなければいけないと感じました。
引用・参考文献
- 対馬栄輝(2020).医療統計解析使いこなし実践ガイド.羊土社,東京.
- 対馬栄輝（2019）.医療系研究論文の読み方・まとめ方.東京図書,東京.
コメント