Last Updated on 2023年12月28日 by カメさん

こんにちは!看護師のカメさん(@49_kame)です。
この記事は5分程度で読めます。

今回は、独立変数(説明変数)と従属変数(目的変数)について解説するよ
独立変数と従属変数は回帰分析の際に使われる用語です。日常では使わない言葉なので耳馴染みがないと思いますので簡単に解説します。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。
独立変数(説明変数)・従属変数(目的変数)とは?
さっそく用語の解説をしていきます。
独立変数(説明変数)
独立変数(independent variable)とは従属変数の原因となる変数のことです。
つまり独立変数は従属変数に影響を与えたり、従属変数を説明したりする変数です。

従属変数(目的変数)を説明するから「説明変数(explanatory variable)」と呼ばれるよ。他にも原因変数や予測変数とも呼ばれるよ。
従属変数(目的変数)
従属変数(dependent variable)とは独立変数の結果となる変数です。
つまり従属変数とは、独立変数の影響を受けて変化する変数です。独立変数の変化により予測されるような測定値と言うこともできます。

独立変数の目的となるから「目的変数(terget variable)」と呼ばれるよ。他にも結果変数、基準変数、外的基準とも呼ばれるよ。
y=a+bxにおける独立変数・従属変数とは?
前述の通り、独立変数と従属変数は回帰分析の際に使用します。回帰分析とは、独立変数が従属変数に及ぼす影響を分析する手法のことです(物事の因果関係を明らかにする分析方法)。
回帰分析の特徴は、回帰式を作成することです。
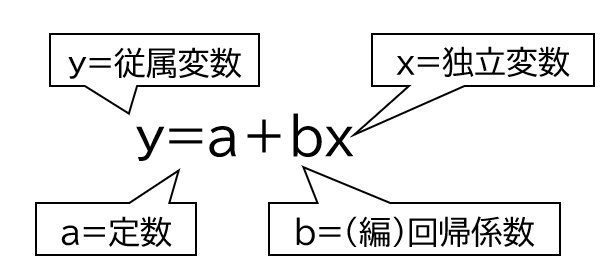
回帰式とは単回帰分析ではy=a+bx 重回帰分析ではy=a+b₁x₁+b₂x₂・・・となります。
上記の図におけるXが独立変数、yが従属変数、aが定数、bが単回帰分析ではあれば回帰係数、重回帰分析であれば編回帰係数となります。
この式から分かることは、2つの変数 XとYは、 Xの値が定まると Yが定まる関係にあると言うことです。

Xが明らかになればY(研究の目的)が明らかになるね
重回帰分析について詳しく知りたい方は下記の記事を参照してください。
【重回帰分析とは?】看護研究の疑問を解決「因果関係を調査しよう」
PICO・PECOから独立変数と従属変数を理解する
独立変数と従属変数を理解するためには、PICO・PECOを用いることが有用です。PICO・PECOについては下記の記事で詳しく解説しています。興味のある方は参照してください。
【PI(E)COとは?】看護師必読「研究疑問を整理しよう!PI(E)COは論文を読む時にも使えるよ」
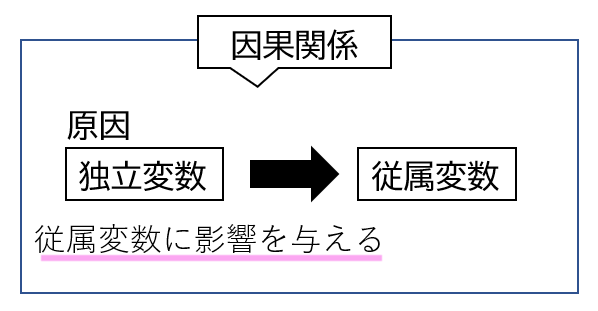
前述のように、独立変数と従属変数は因果関係を推定する際に使用します。そして、因果関係の原因が「独立変数」であり、その結果が「従属変数」です。
PICO・PECOについて考えると、原因、つまり結果に影響を与える因子である「独立変数」は、I(intervention:介入)またはE(exposure:暴露)に該当します。
病棟の騒音・照明が、患者の睡眠時間に影響を及ぼしているかを明らかにしたい場合は病棟の騒音・照明がE(exposure:暴露)であり、「独立変数」となります。
また、結果である「従属変数」はPICO・PECOにおけるO(outcome:結果)の部分に該当します。
上記と同様に、病棟の騒音・照明が、患者の睡眠時間に影響を及ぼしているかを明らかにしたい場合は、患者の睡眠時間がO(outcome:結果)であり「従属変数」です。
実際の論文で独立変数と従属変数を見てみよう
それでは実際の論文で独立変数と従属変数を見てみましょう。
この論文は、ドナーおよびその家族への看護実践における看護師の不全感とその影響要因を明らかにする研究です。
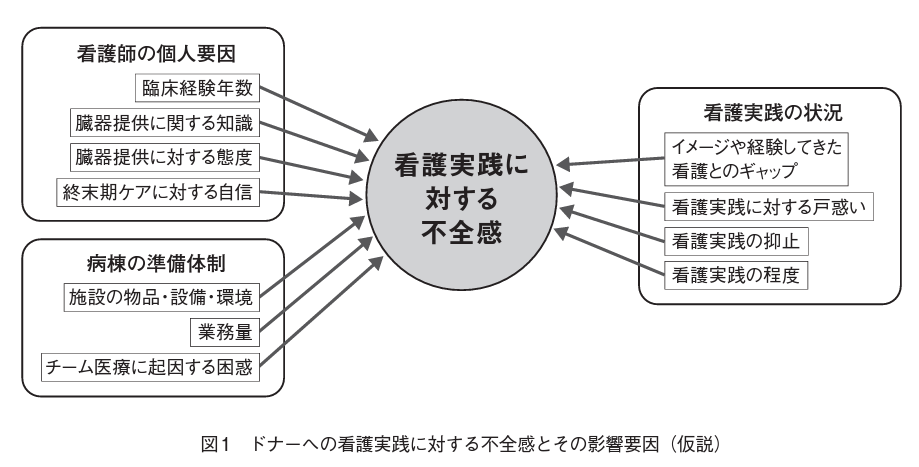
この研究の仮説は以下の図になります。
結果が看護実践に対する不全感で、影響する要因が看護師の個人要因、病棟の準備体制、看護実践の状況です。
つまり、看護実践に対する不全感が結果であり「従属変数」となります。また看護師の個人要因、病棟の準備体制、看護実践の状況は影響する要因であり「独立変数」です。
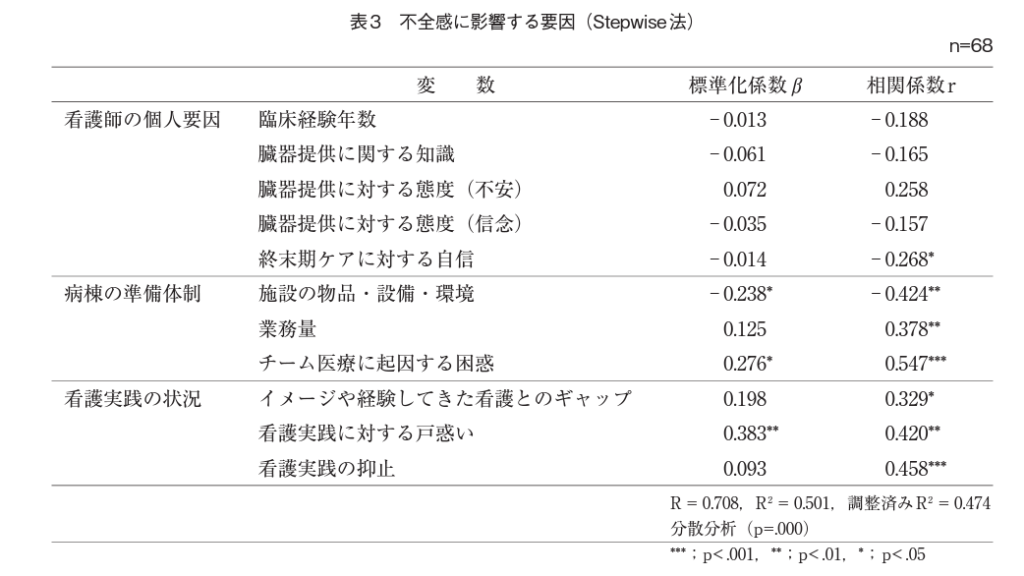
ちなみに、上記の因果関係を明らかにした重回帰分析の結果が以下の表になります。
重回帰分析については下記で詳しく解説しています。良かったら参照してください。
【重回帰分析とは?】看護研究の疑問を解決「因果関係を調査しよう」
まとめ

独立変数と従属変数は論文の要になると言われています。独立変数と従属変数を明確にし、それを基に議論を展開していくことで、論旨が一貫した論文になります。

因果関係を明らかにするような研究を行う際も、読む際も、それぞれの変数の役割を明確にしながら読むようにしよう。
この記事を読んだ方におすすめの書籍を下記で紹介しています。良かったら参照してください。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。














コメント