Last Updated on 2024年4月6日 by カメさん

こんにちは!看護師のカメさん(@49_kame)です。
この記事は5~6分で読めます。

今回は統計解析ソフトEZRを使用して相関分析を行う方法を解説します
相関分析は看護研究において重要な役割を果たします。変数間の関連性を明らかにし、より良い看護介入策を導き出すためには、相関分析の統計手法を理解することが不可欠です。本記事では、相関と相関係数について簡単に解説した上でEZRを使用して相関分析を行う方法を解説します。初学者にも分かりやすく解説しています。あなたの研究の参考になれば幸いです。
このブログでは統計解析ソフトしてEZRを使用しています。EZRは無料かつ精度も高い統計解析ソフトであるためおすすめです。EZRの概要とインストール方法については【EZRの概要とインストール方法】看護研究を変える!EZRで効率的な統計解析を参照してください。
はじめに

まずは相関分析を行うための基礎知識を解説します
相関分析とは?
相関分析とは、2つのデータの関係性の強さを分析する方法です。一方が変化すると他方も一定の傾向で変化する関係があります。つまり1つのデータが大きくなったり小さくなったりすると、もう1つのデータも大きくなったり小さくなったりするということです。
この関係性を把握することで、一つの変数の動向から他の変数の挙動を予測することが可能になります。看護研究では、例えば、歩数が増えると睡眠時間が長くなる関係性など患者の生活習慣と健康状態の間にどのような関係があるのかを調べることに用いられます。
また相関分析では散布図を求めることもあります。散布図とは、下記のような縦軸と横軸のある図のことです。
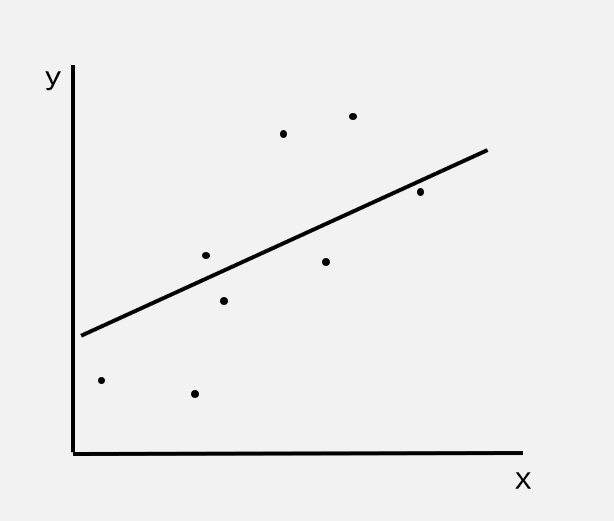
散布図は、あるデータを元にして縦軸と横軸の2つの項目で量を計測し、分布を表現するために使うグラフです。グラフに記載してある線は、この点がどのような関係性があるかを示したものになります。
この線が右肩上がりの場合が正の相関、右肩下がりの場合が負の相関を表します。この場合、Xが増えるにつれて、Yも増える関係であることが分かります。

相関分析では相関係数を計算し、関係の強さを求めるよ!
※相関分析の注意点
相関分析の注意点は相関分析は因果関係は分からないということです。相関分析では、 AだからBという原因(因果関係)を探索することはできません。
例えば、歩数が原因で睡眠時間が結果であるというような議論はできません。あくまで相関分析は関係性の議論だけです。因果関係を探索するためにはy=a+bXの式を作る回帰分析等の分析方法が必要です。
回帰分析について詳しく知りたい方は【重回帰分析とは?】看護研究の疑問を解決「因果関係を調査しよう」を参照してください。
相関係数とは?
相関分析では相関係数を求める場合が多いです。相関係数は、二つの変数間の相関の強さと方向を数値で表したものです。
相関係数には種類がある
相関係数には2つの種類があります。分析したデータのうち、少なくとも1つのデータが正規分布していない場合はSpearmanの順位相関係数を使用します。またどちらのデータも正規分布している場合はPearsonの相関係数を使用します。
相関係数の大きさの判断
相関係数にはマイナスやプラスがあり、それぞれ、マイナスが負の相関関係・プラスが正の相関関係と呼ばれています。正の相関とは「片方の値が増加すると、もう一方も増加する」関係のことです。一方で、負の相関とは、「片方の値が増加すると、もう一方が減少する」関係のことです。

運動時間が増加すると睡眠時間も増加するのは正の相関関係だよ!
相関係数は1からー1で評価します。相関係数が1もしくは-1に近づくほど関係が強くなり、0に近づくほど関係が弱くなります。
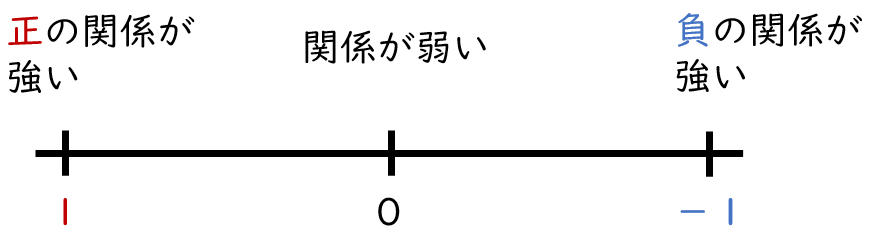
また、相関係数には下記のような判断基準があります。この基準は便利ですが、あくまで目安です。そのため、先行研究や自身の臨床経験を基にデータを解釈するようにしましょう。


ちなみになぜ絶対値で記載されているかというと、rにはマイナスやプラスがあるけど、数字の大きさは同じだからだよ。
相関分析の概要を知りたい方は【相関てなんだ?】看護研究の疑問を解決「2つの変数の関係性を確認しよう」を参照してください。
EZRで行う相関分析の手順
それではEZRを使用して相関分析を行う手順を解説します。
今回使用するデモデータ
今回は下記のデモデータを使用します。
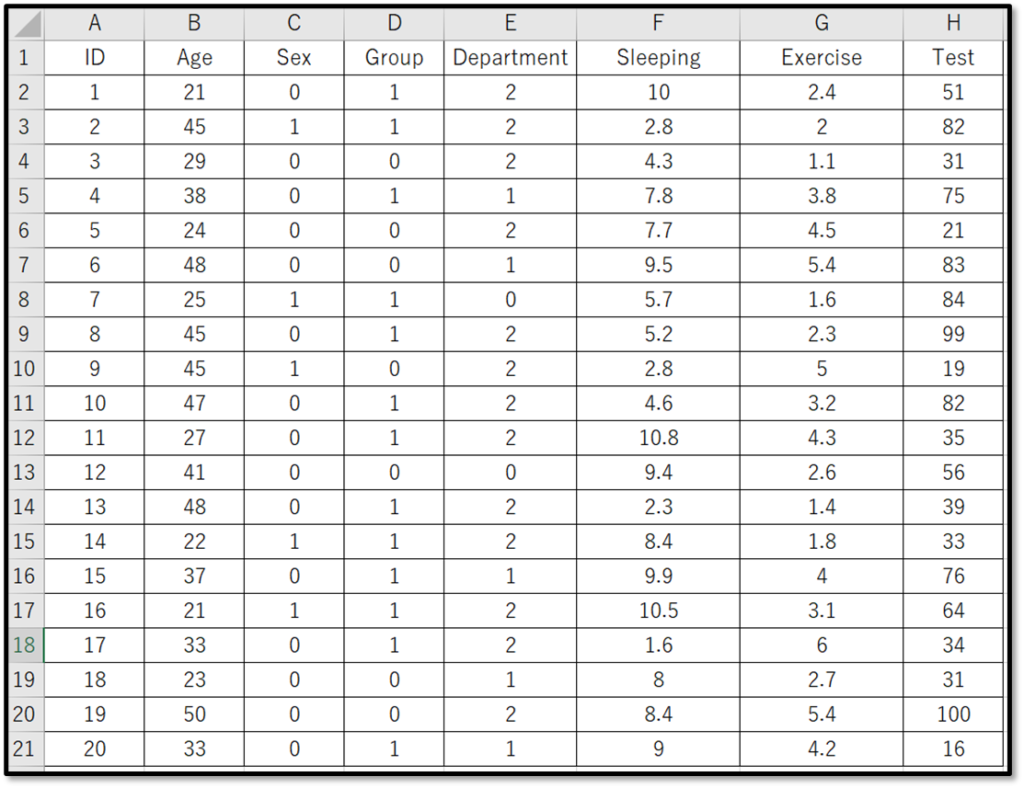
表示しているのは、デモデータの一部です。デモデータは下記からダウンロードできるので使ってみてください。

ランダム関数で作成しているため、今回の結果とズレが出るかもしれませんが、ご了承ください。
こちらのデモデータを読み込んだ後の段階から解説します。データの読み込み方法については、【統計解析ソフトにデータを入力】看護研究初めの一歩:EZRにデータセットを入力しよう!を参照してください。
今回はデモデータのうち、「Sleeping(睡眠時間)」と「EXercise(運動時間)」「Test(テストの点数)」しか使用します。
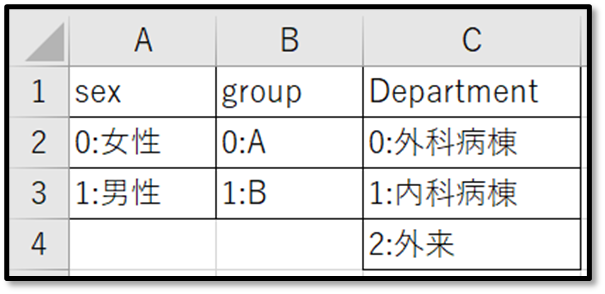
ちなみにSex(性別)、Group、Department(部署)については下記のようにコード化しています。今回のデモデータを他の分析の練習に使用する際は参照してください。
相関分析の検定実行手順
下記が相関分析の検定の手順です。今回は上記のデモデータの「Sleeping(睡眠時間)」×「Test(テストの点数)」の比較と、「EXercise(運動時間)」×「Test(テストの点数)」の比較を行いながら解説していきたいと思います。
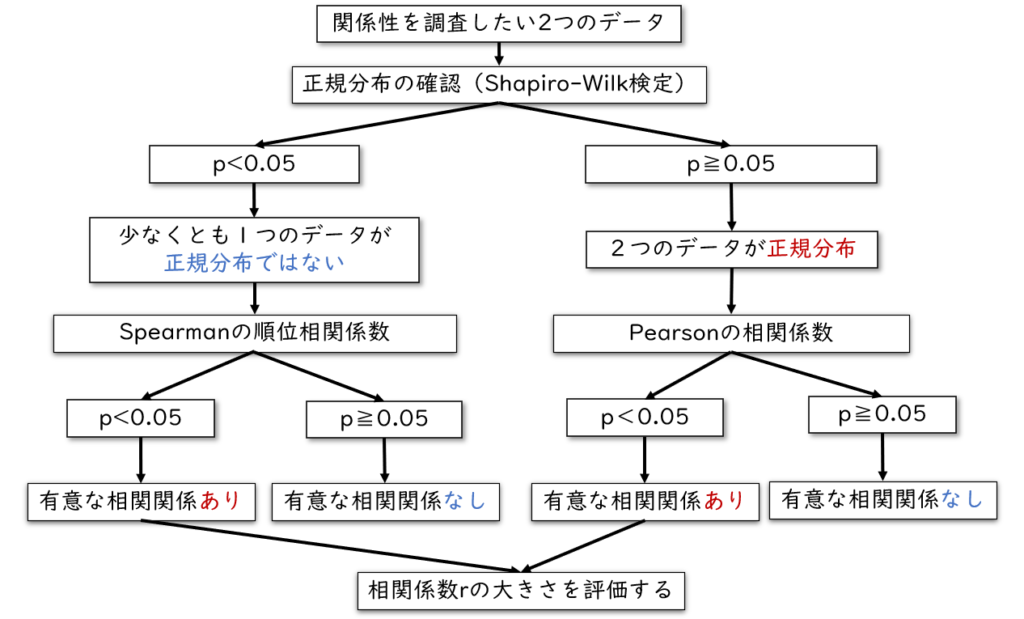
「Sleeping(睡眠時間)」×「Test(テストの点数)」、「EXercise(運動時間)」×「Test(テストの点数)」についてそれぞれ正規分布を確認する必要がありますが、今回は正規分布の確認手順は割愛します。詳しく知りたい方は【正規分布とは?:実践編】看護研究の疑問を解決「EZRで正規分布を確認しよう」を参照してください。

デモデータでは「Sleeping(睡眠時間)」×「Test(テストの点数)」がどちらも正規分布になるように、「EXercise(運動時間)」×「Test(テストの点数)」はEXerciseが正規分布にならないように調整しているよ。
正規分布の場合の相関分析
それでは「Sleeping(睡眠時間)」×「Test(テストの点数)」の関係を見て行きましょう。テストの点数と睡眠時間が関係しているかどうかということです。前述の通り、これら2つの変数は、どちらも正規分布になるように事前に調整してあります。
どちらも正規分布している場合は、Pearsonの相関係数を使用します。
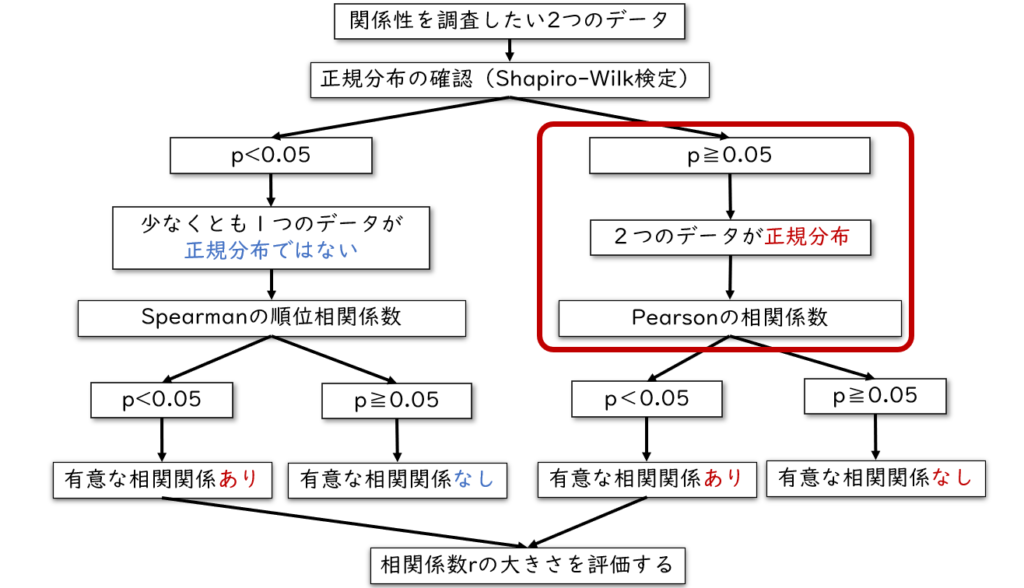
それではPearsonの相関係数を用いて相関分析を行う方法を解説します。「統計解析」→「連続変数の解析」→「相関係数の検定(Pearsonの積率相関係数)」の順に選択します。
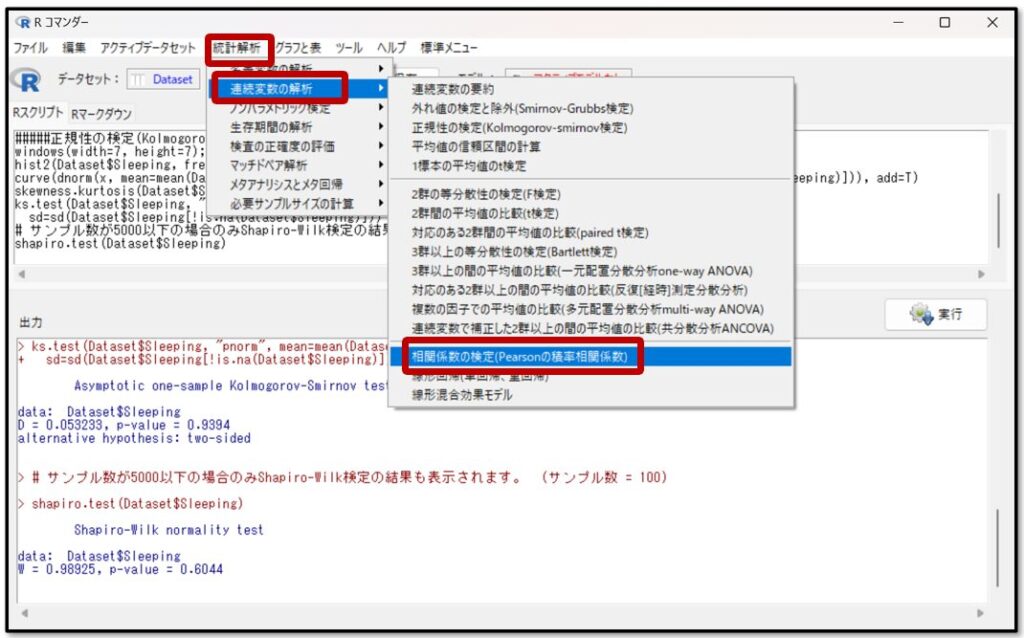
次に変数の選択で、今回相関関係を確認したい変数である、SleepingとTestを選択します。

コントロールキーを押しながら選択することで、2つの変数を選択することができるよ!
下記がEZRの出力結果です。相関分析の際は、散布図も出力されます。
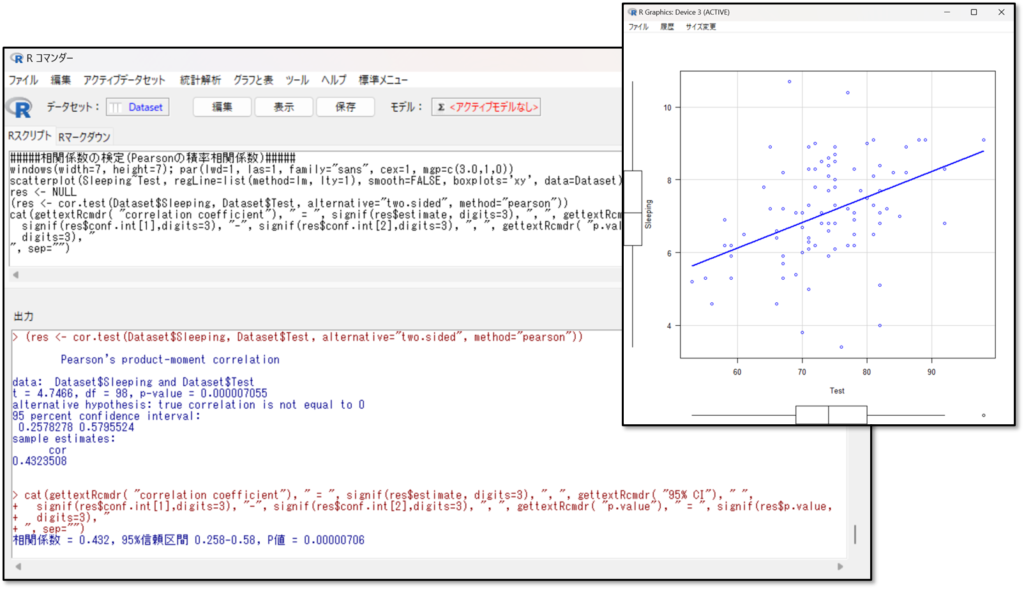
出力結果の見方を解説します。散布図が出力されるので、まずは視覚的に相関関係を確認しましょう。次に「p-value(p値)」と「95 percent confidence interval(95%信頼区間)」、「cor(相関係数)」を確認します。p値がp<0.05であれば、有意な相関があると判断します。また95%信頼区間は真の値が95%の確率で入る範囲のことです。相関係数については上記の相関係数の判断基準を参考に解釈しましょう。
今回の結果を改めて見てみましょう。まずは散布図の結果を確認します。
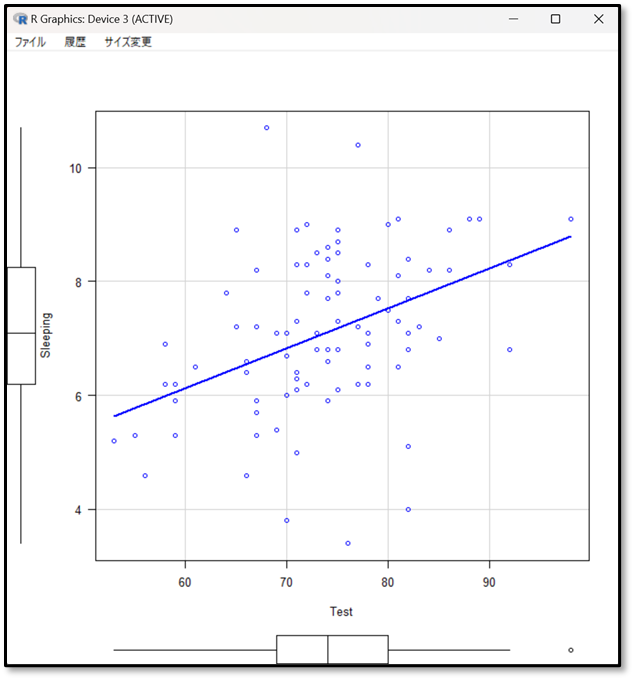
この散布図は縦が睡眠時間、横がテストの点数になっています。ゆるやかに上がっているので睡眠時間が上がれば、テストの点数が少し上がる関係であることがわかります。
次にp値と95%信頼区間、相関係数の結果を見てみましょう。
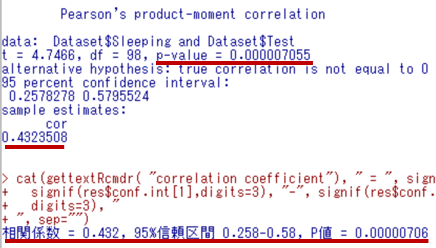
p-value(p値)を見ると0.0000007055となっています。pが0.05未満(p<0.05)なので、有意な相関があると判断します。次に相関係数(cor)を確認します。相関係数は0.4323508と出力されています。相関係数の95%信頼区間は0.258-0.58であり、95%の確率で真の値が、この範囲に当てはまることが分かります。相関の大きさについては、今回の相関係数を上記の判断基準に照らすと、かなり相関関係があることが分かります。また今回の相関係数にはー(マイナス)がついていないため、正の相関関係であることが分かります。つまり、片方が上がれば、片方も上がる関係です。

ちなみに相関係数を研究結果で記載する際はcorではなくて、r=で大丈夫だよ
少なくとも1つのデータが正規分布でない場合の相関分析
それでは「Exercise(運動時間)」×「Test(テストの点数)」の関係を見て行きましょう。テストの点数と運動時間が関係しているかどうかということです。前述のデモデータにおいて、Exercise(運動時間)が正規分布しないように事前に調整してあります。つまり、「Exercise(運動時間)」が正規分布ではなく、「Test(テストの点数)」が正規分布するように調整しています。

興味のある人は、デモデータで相関分析する前に正規分布の確認もしてみてね。正規分布の確認方法については【正規分布:実践編】EZRで正規分布を確認しよう!を参照してね。
話を戻します。上記のように、少なくとも1つのデータが正規分布でない場合はSpearmanの順位相関係数を使用します。
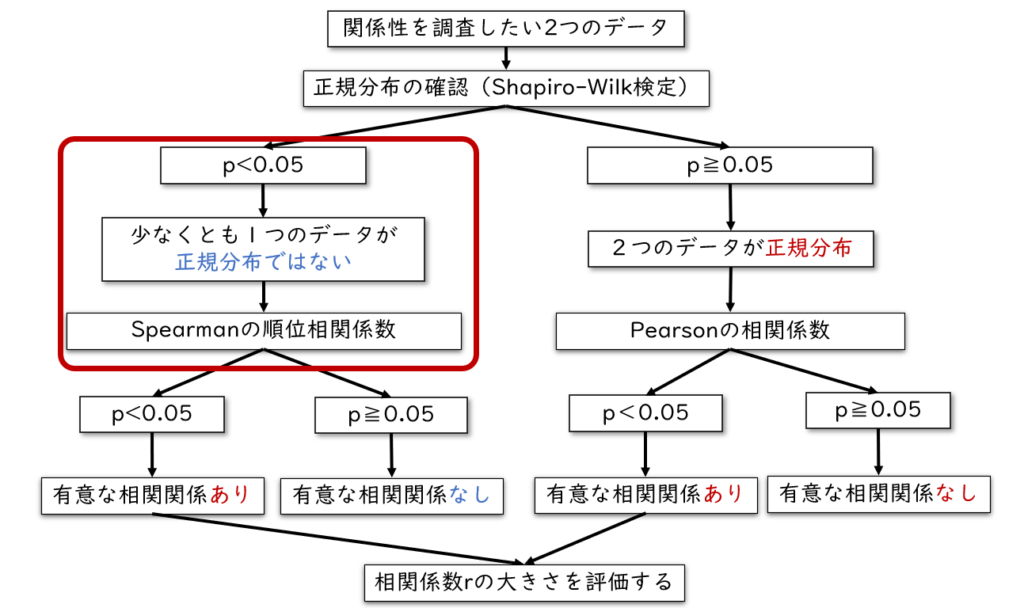
それでは、Spearmanの順位相関係数を使用した相関分析の方法を解説していきます。EZRの操作画面で「統計解析」→「ノンパラメトリック検定」→「相関係数の検定(Spearmanの順位相関係数)」を選択しましょう。
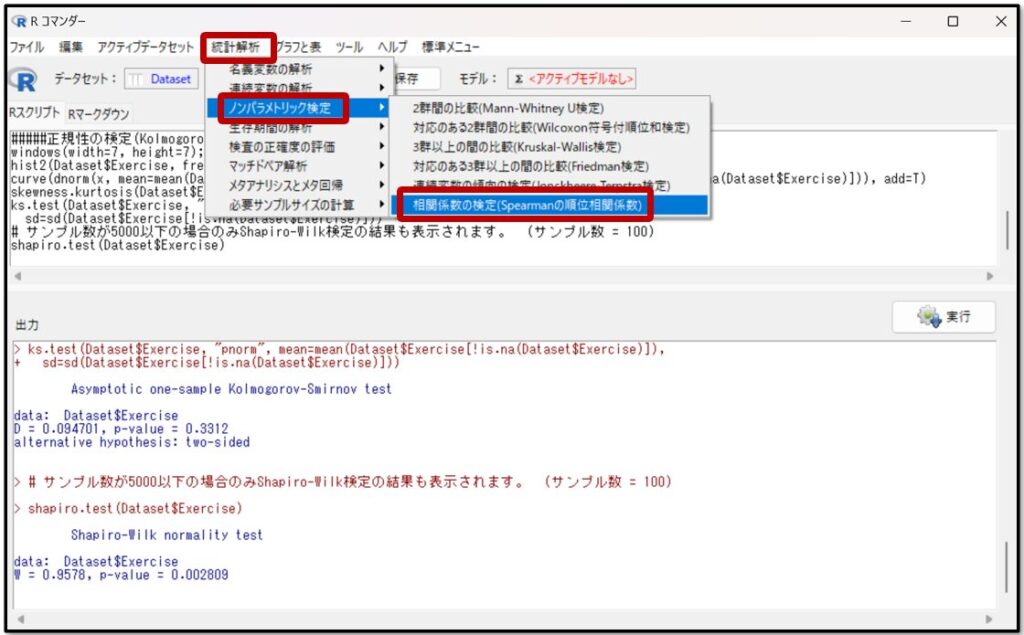
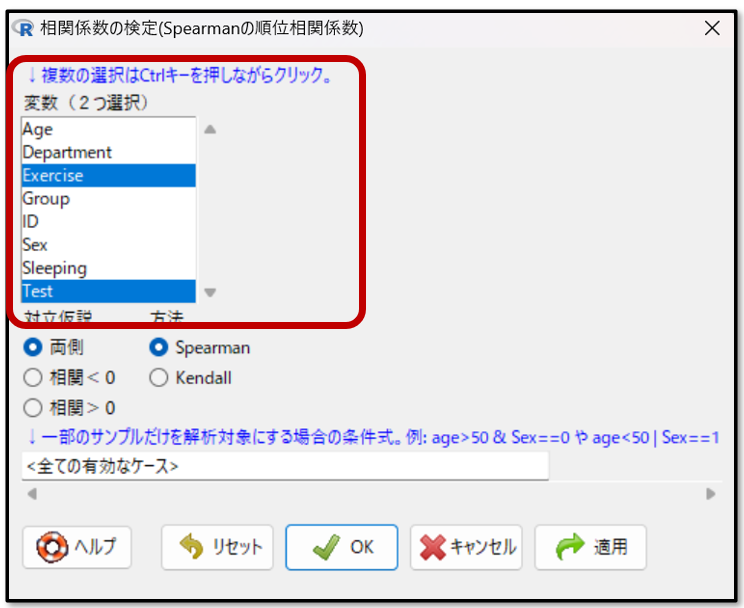
続いて変数として、今回相関関係を確認したい「Exercise(運動時間)」と「Test(テストの点数)」を選択します。
下記が、「Exercise(運動時間)」と「Test(テストの点数)」の相関関係を検定した結果です。
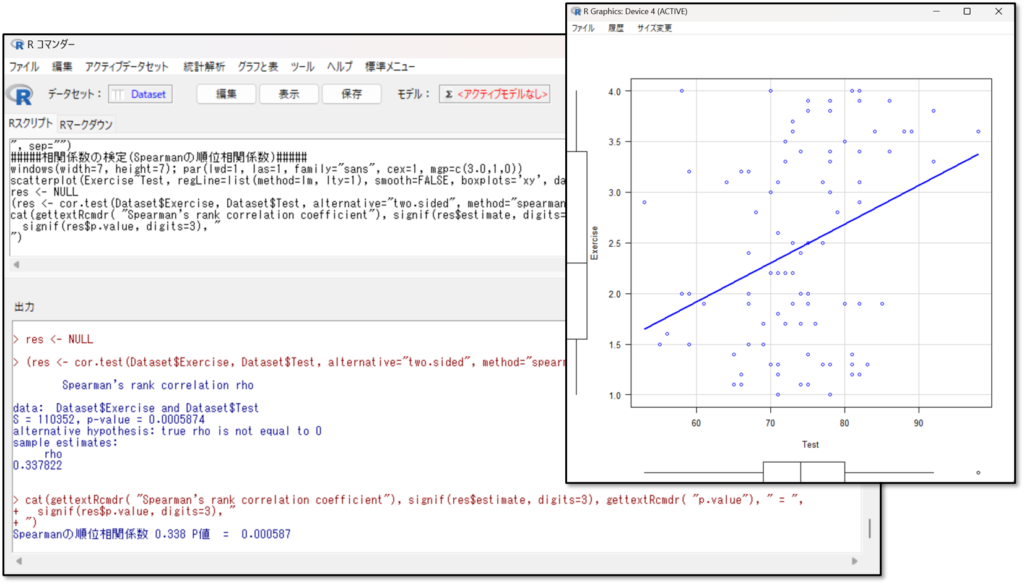
結果の見方を解説します。散布図が出力されるので、まずは視覚的に相関関係を確認しましょう。次に「p-value(p値)」と「rho(相関係数)」を確認します。先ほどのPearsonの相関係数を使用した相関分析では、相関係数がcorと記載されていましたが、Spearmanの相関係数を使用した相関分析では、相関係数がrhoで表現されます。p値がp<0.05であれば、有意な相関ありと判断します。相関係数については、先ほど同様に前述の相関係数の判断基準を参考に解釈しましょう

ちなみに95%信頼区間はノンパラメトリック法では算出されないよ
それでは今回の出力結果を改めて見てみましょう。まずは散布図から確認します。
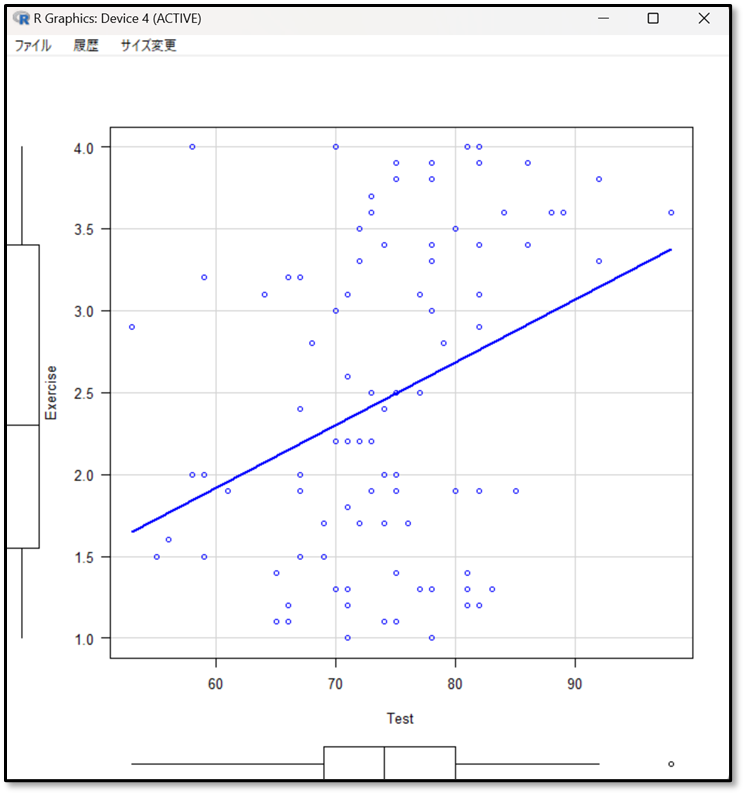
散布図は、ゆるやかに右に上がっているので、正の相関関係です。つまり「Exercise(運動時間)」が上がれば、「Test(テストの点数)」も上昇する関係です。
次にp値と相関係数も見てみましょう。

p-value(p値)を見ると0.0005874と出力されています。つまりp値が0.05未満なので、有意な相関関係があると判断します。次に相関係数も見てみましょう。rhoのところを確認すると、0.337822と出力されています。相関係数の判断基準をから考えると、やや相関関係があることがわかります。ちなみに、散布部が右肩下がりで、相関係数にーがついている場合は、負の相関関係と判断します。片方が下がれて、片方も下がる関係です。
負の相関関係の場合の例
負の相関関係とは片方が減少すれば、片方も減少する関係です。負の相関関係の場合は散布図が右肩下がりとなり、相関係数にーがつきます。下記が負の相関関係の場合の例です。
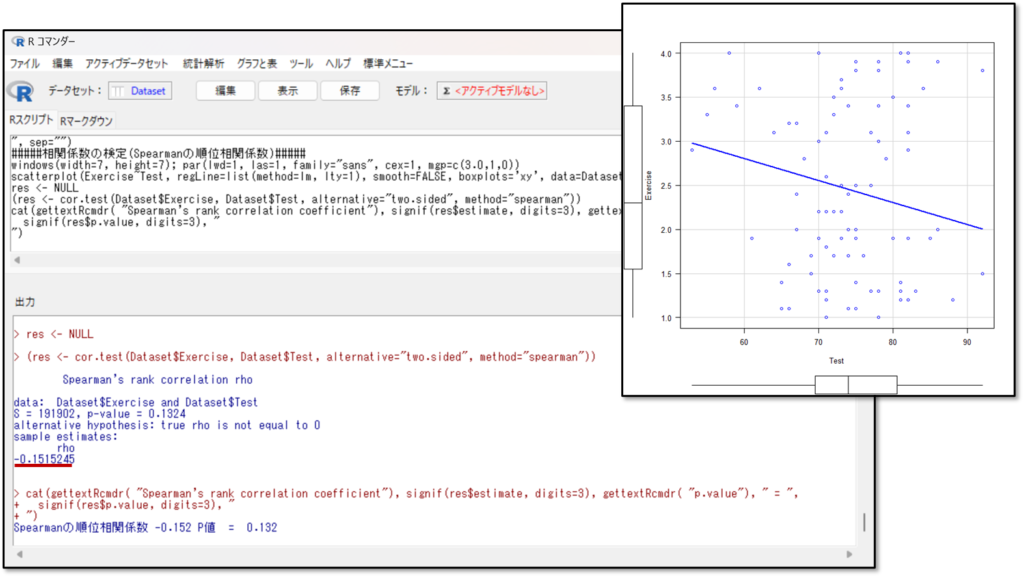
上記の例だと散布図が右肩下がりで、相関係数もー0.132と、マイナスがついています。そのため、負の相関関係があると判断します。

前述のデモデータの「デモデータ2」は負の相関関係になるように調整しているから興味のある人はやってみてね。
まとめ

相関分析は、看護研究における重要な統計的手法の一つです。正しい相関係数の選択と適切な分析手順によって、信頼性の高い結果を得ることができます。この記事が、相関と相関係数の理解を深め、実際の研究に役立てるための一助となれば幸いです。

あなたの研究が成功することを願っています。
今回は相関分析を実際に行う具体的な方法を解説しました。相関分析の概要を知りたい方は下記を参照してください。











コメント