Last Updated on 2024年3月30日 by カメさん

こんにちは!看護師のカメさん(@49_kame)です。
この記事は5~6分で読めます。

今回は統計解析ソフトEZRを使用して実際に2群の差の検定(対応のないデータ)を行う方法を解説します
2つのグループ間の平均値に差が存在するかどうかを明らかにすることは、多くの科学的研究の基盤となります。この記事では、初心者でも理解しやすいように、統計解析ソフトEZRを用いた2標本の差の検定の基本的な手順と結果の解釈方法を、具体例を交えて詳しく解説していきます。この記事が統計的な手法に新しい一歩を踏み出すあなたのサポートになれば幸いです。
このブログでは統計解析ソフトしてEZRを使用しています。EZRは無料かつ精度も高い統計解析ソフトであるためおすすめです。EZRの概要とインストール方法については【EZRの概要とインストール方法】看護研究を変える!EZRで効率的な統計解析を参照してください。
はじめに

まずは2標本の差の検定を行うための基礎知識を解説します
2標本の差の検定とは?
2標本の差の検定は、対応のない(独立した)グループまたは対応のあるグループの平均値に統計的に有意な差があるかどうかを評価する方法です。この手法は科学的研究における仮説検定に広く用いられています。事前に帰無仮説と対立仮説を設定し、検定を行います。
2標本の差の検定の概要を知りたい方は【t検定ってなに?:概要編】看護研究の疑問を解決「2群の差を比較しよう」を参照してください。
帰無仮説と対立仮説とは?
帰無仮説と対立仮説は統計解析の際に立てる仮説のことです。帰無仮説は否定(棄却)されることを期待して設定され、対立仮説は採択されることを期待されて設定されます。統計解析では一般的に、p<0.05の場合に帰無仮説が棄却されます。
例えば、2群の差を調べる場合は、帰無仮説「差が無い」と対立仮説「差があるの2つの仮説」を立てます。差があるか知りたい検定なので、帰無仮説である差が無いが否定されることが期待されています。つまり差がない仮説が否定されて差がある結果になったらいいなあということです。
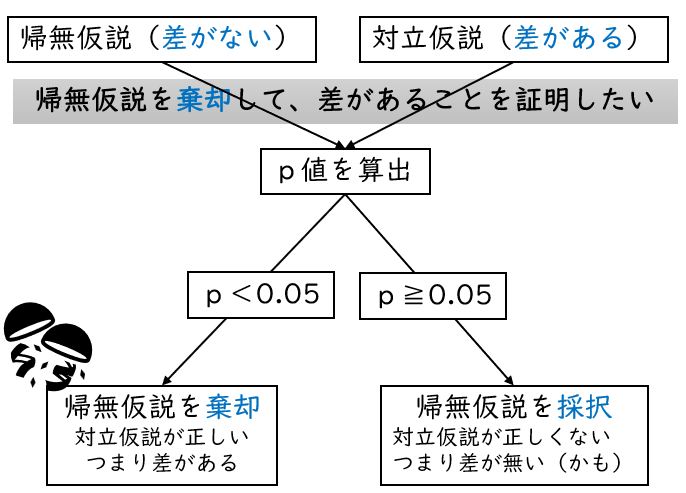
そして結果を統計解析を使用して確認します。p値が0.05未満であれば、帰無仮説が棄却、つまり否定されます。帰無仮説 差がないという仮説が否定されたということは、2群には差があるあることが分かったということです。反対にpが0.05以上であれば、帰無仮説である、差が無いという仮説が選ばれてしまうので、2群には差が無かったという結果になります。

ここは、混乱してしまう人も多いと思うので、ゆっくり考えてみてください。
対応のないデータと対応のあるデータとは?
対応のないデータとは、互いに独立した2つのグループ間で比較が行われる場合です。また対応のあるデータは、同じ被験者が異なる条件下で測定されたデータなど、ペアで存在するデータを指します。
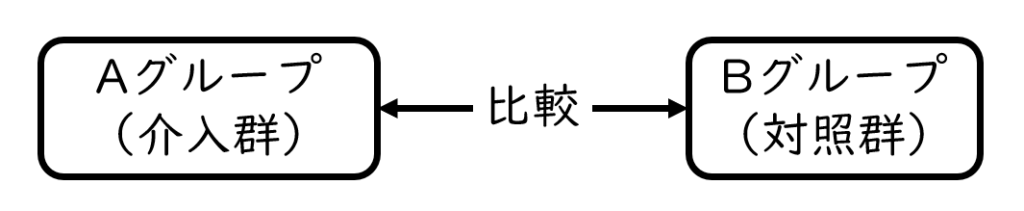
対応のないデータの2標本の差の検定とは?
対応のないデータを用いた2標本の差の検定とは、2つのグループからそれぞれ収集するデータを比較する分析のことです
例えば、介入群と対照群の2群を比較する分析などです
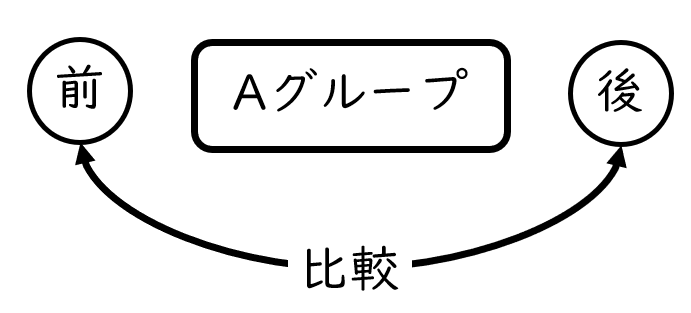
対応のあるデータの2標本の差の検定とは?
対応があるデータを用いた2標本の差の検定とは、1つのグループから収集する2つのデータを比較する分析のことです
例えば、1グループへの介入前後の点数の比較などです
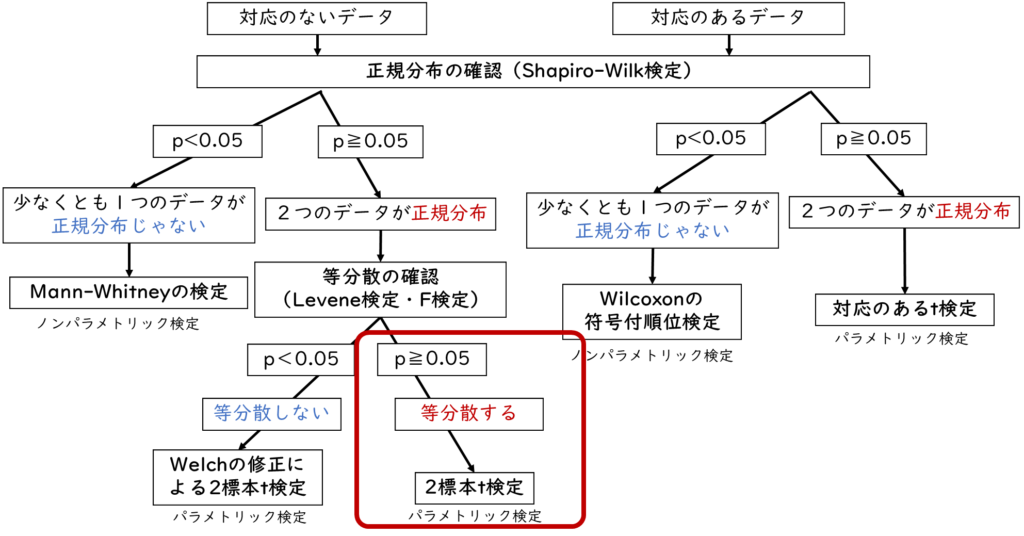
2標本の差の検定には種類がある
2標本の差の検定には種類があり、以下の3つのポイントで決まります。
- ➀ 「対応のないデータ」or 「対応のあるデータ」
- ② 「正規分布」 or 「正規分布でない」
- ③ 「等分散する」or 「等分散しない」


収集したデータの特徴に合わせて分析方法を検討しよう。今回は対応のないデータに焦点を当てて解説するよ。
EZRで行う2標本の差の検定手順(“対応のない”データ)
今回はEZRを使用して「対応のないデータ」の2標本の差の検定について解説します。
今回使用するデモデータ
今回は下記のデモデータを使用します。
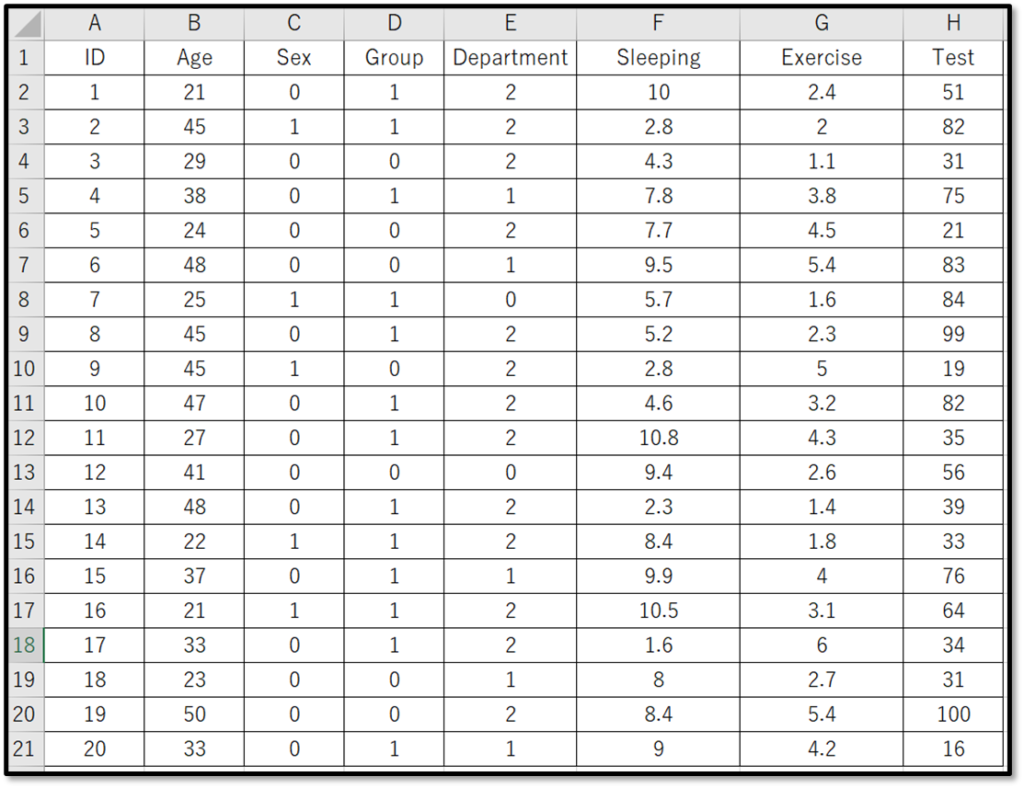
表示しているのは、デモデータの一部です。デモデータは下記からダウンロードできるので使ってみてください。

ランダム関数で作成しているため、今回の結果とズレが出るかもしれませんが、ご了承ください。
こちらのデモデータを読み込んだ後の段階から解説します。データの読み込み方法については、【統計解析ソフトにデータを入力】看護研究初めの一歩:EZRにデータセットを入力しよう!を参照してください。
対応のないデータとして、グループABのテストの点数を比較します。今回のデモデータはすでにコード化しているので、01のデータになっています。グループのコード化は、0がAグループ、1がBグループです
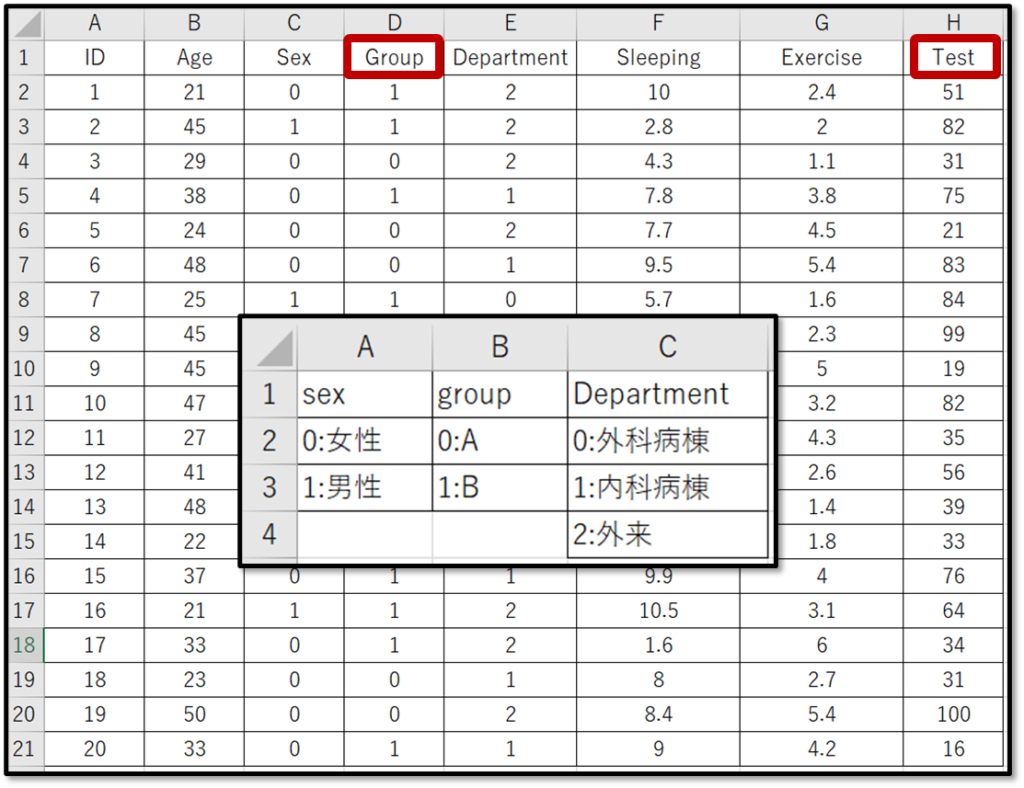
「対応のないデータ」の2標本の差の検定実行手順
下記が2標本の差の検定の手順で、対応のないデータの2標本の差の検定について手順通りやってみたいと思います。今回は上記のデモデータのグループA(0)とグループB(1)の比較を行ってみたいと思います。
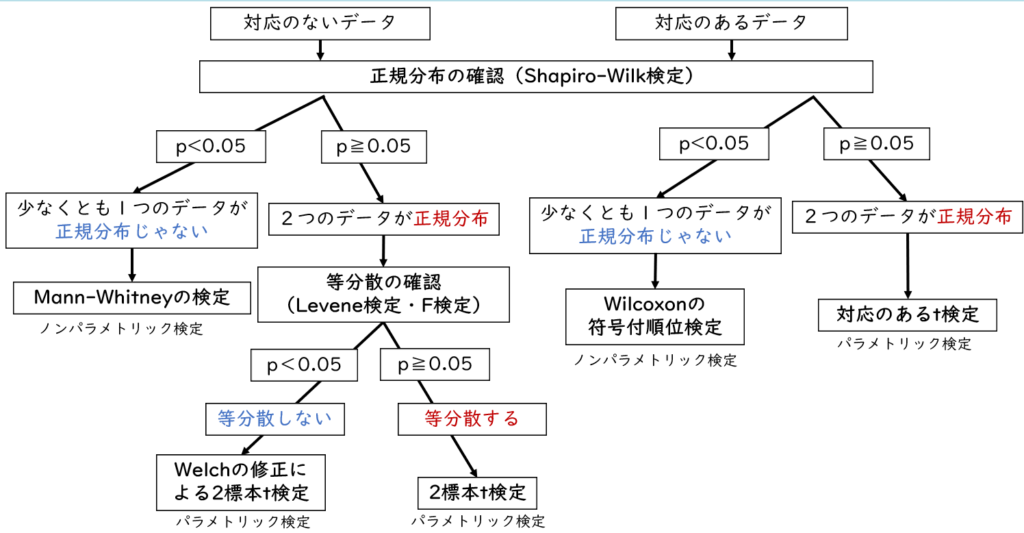
まずはAグループとBグループのテストの点数についてそれぞれ正規分布を確認します。今回は正規分布の確認手順は割愛します。詳しく知りたい方は【正規分布とは?:実践編】看護研究の疑問を解決「EZRで正規分布を確認しよう」を参照してください。
2標本ともに正規分布している場合
AグループとBグループの両方が正規分布していた場合、次は等分散の確認をおこないます。
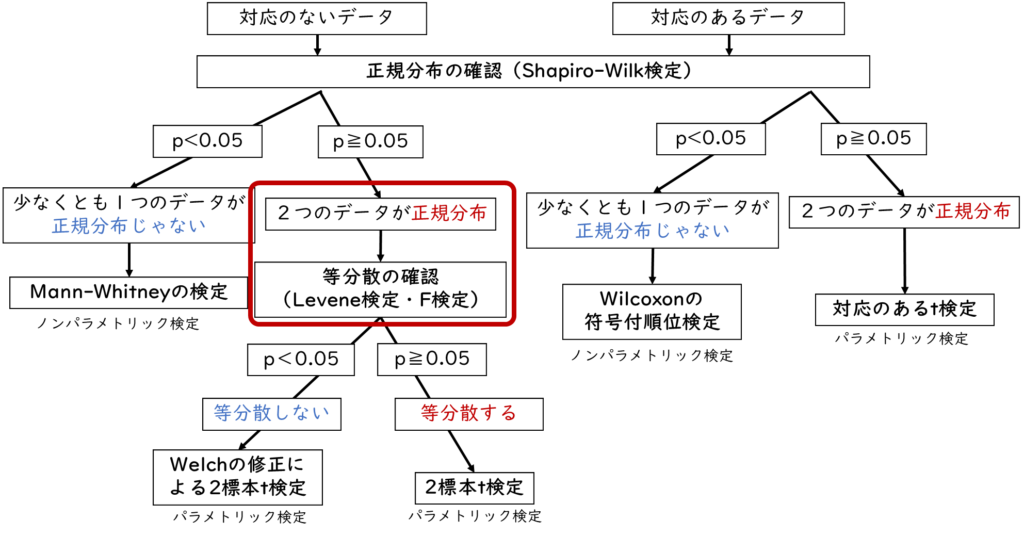

デモデータの中の「データ1」と記載されたデータが2標本ともに正規分布になるように調整したデータだよ。
分散の検定は「統計解析」→「連続変数の解析」→「2群の等分散性の検定(F検定)」を選択します。
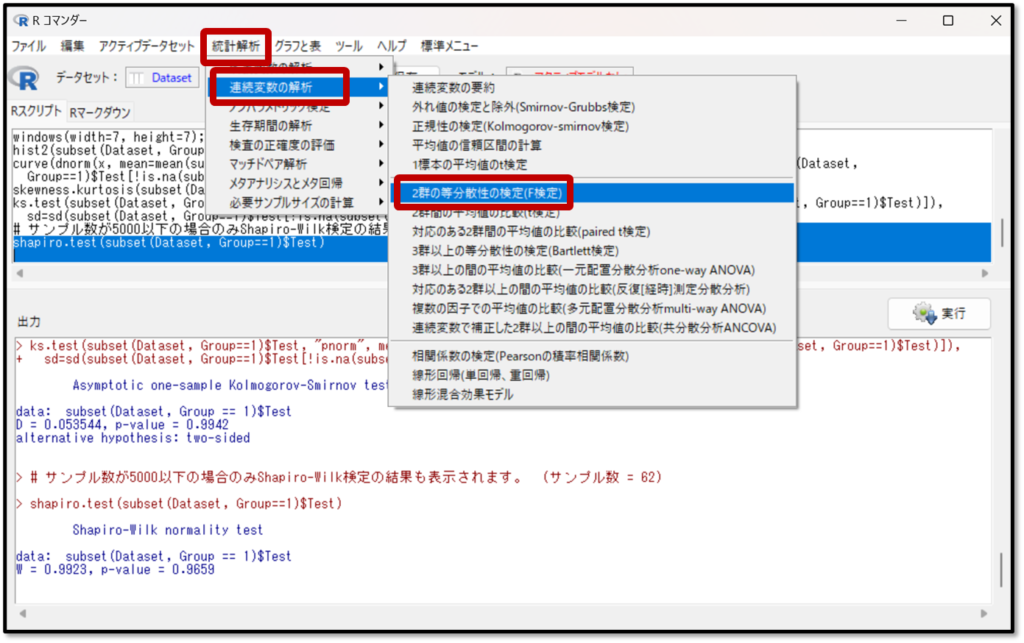
次に「2群の等分散性の検定(F検定)」をしたい変数を選択します。目的変数には、今回比較したいテストの点数を選択します。そして、比較するのがグループなので、グループを選択します。OKを押すと等分散性の検定の結果が算出されます。
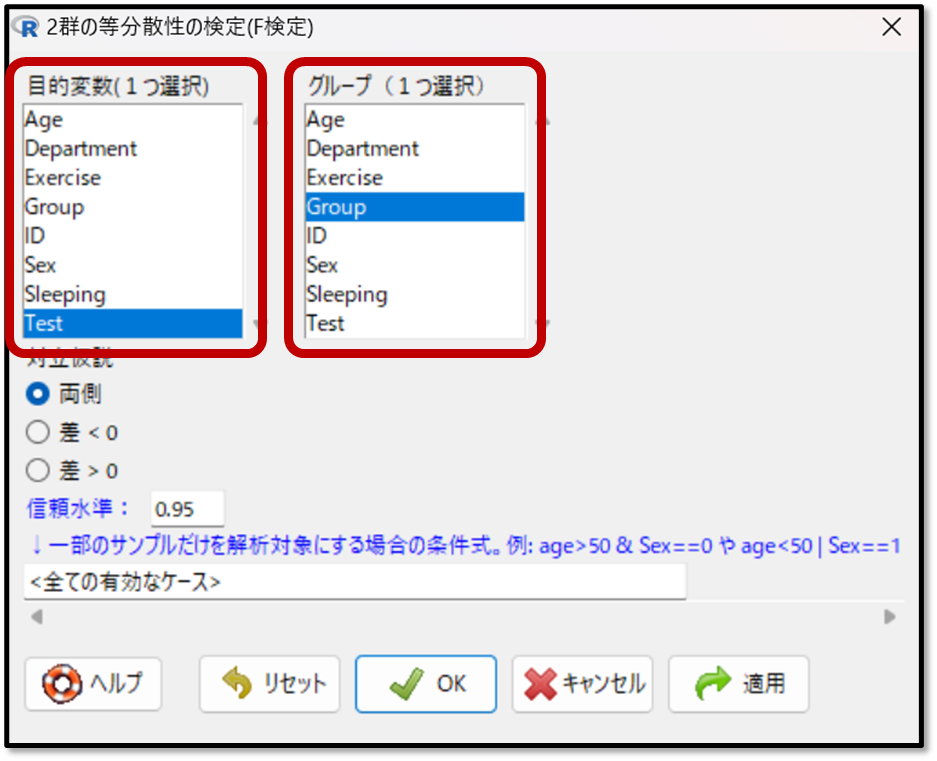
下記が「2群の等分散性の検定(F検定)」の結果です。
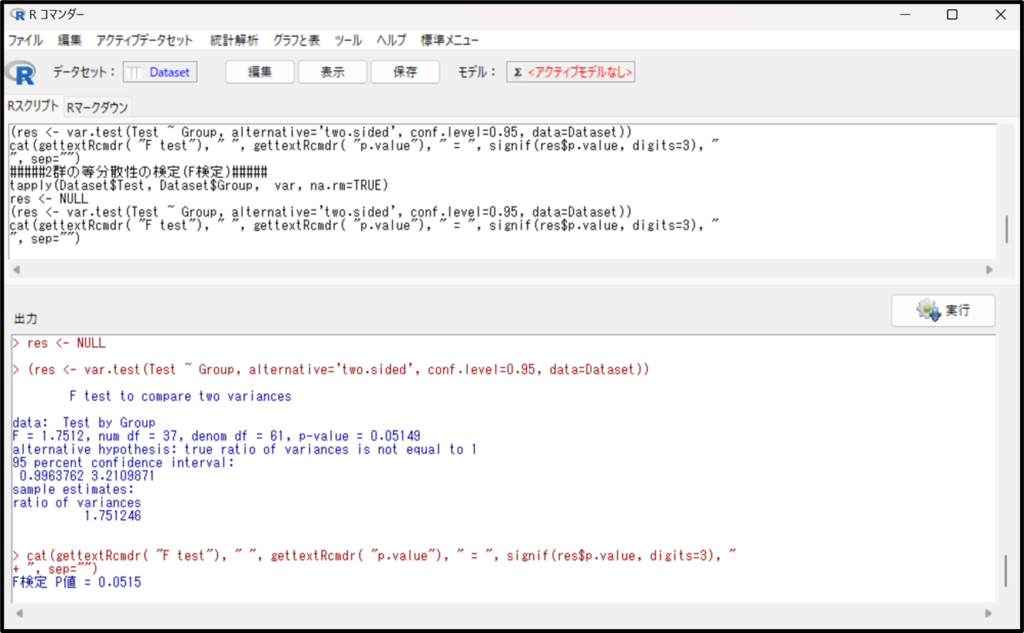
pバリューに注目します。
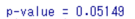
pバリューは0.05149、pが0.05以上なので等分散していると判断します。等分散しているということは、使用する検定は2標本t検定ですね。
2標本t検定の方法は、「統計解析」→「連続変数の解析」→「2群間の平均値の比較(t検定)」を選択します。
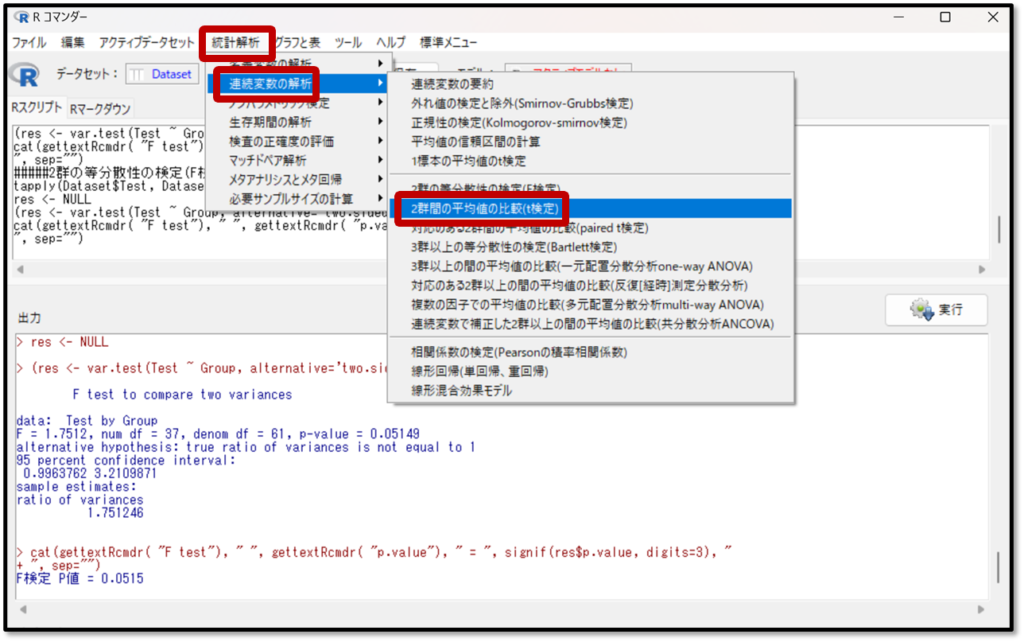
次に「2群間の平均値の比較(t検定)」をしたい変数を選択します。目的変数として、今回比較したいテストの点数を選択します。比較する群には今回比較するグループを選択します。最後に等分散と考えますか?の はい を選択します。これでOKを選択するとt検定の結果が算出されます。
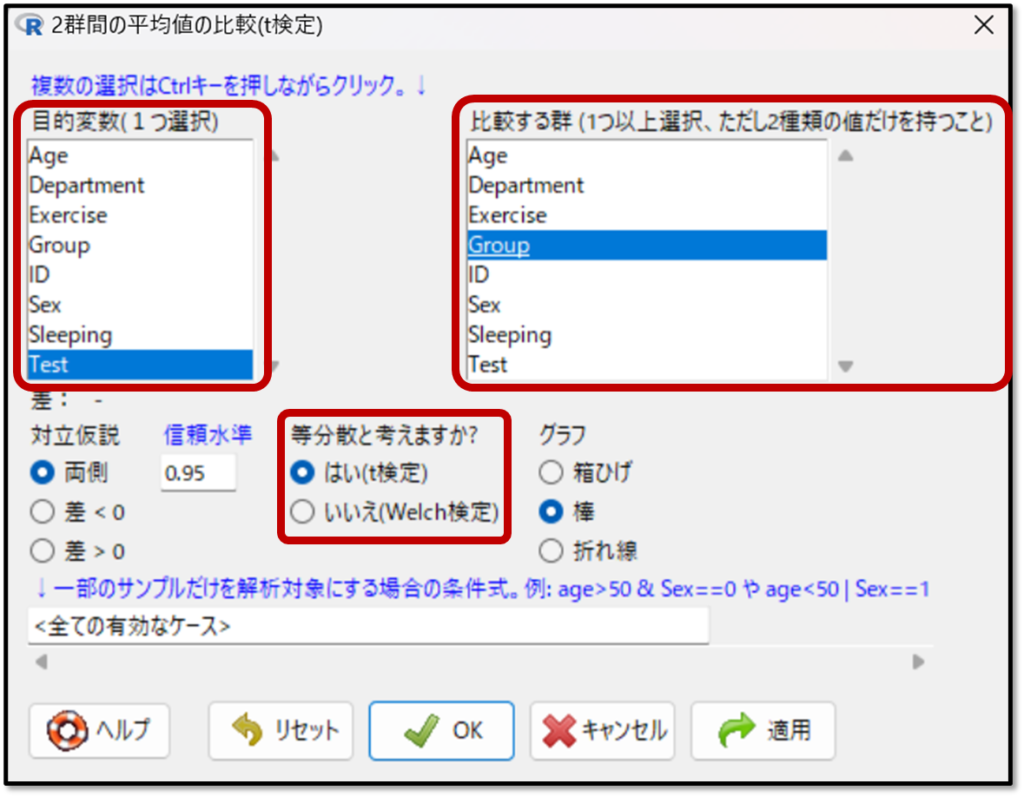
下記がt検定の出力結果です。
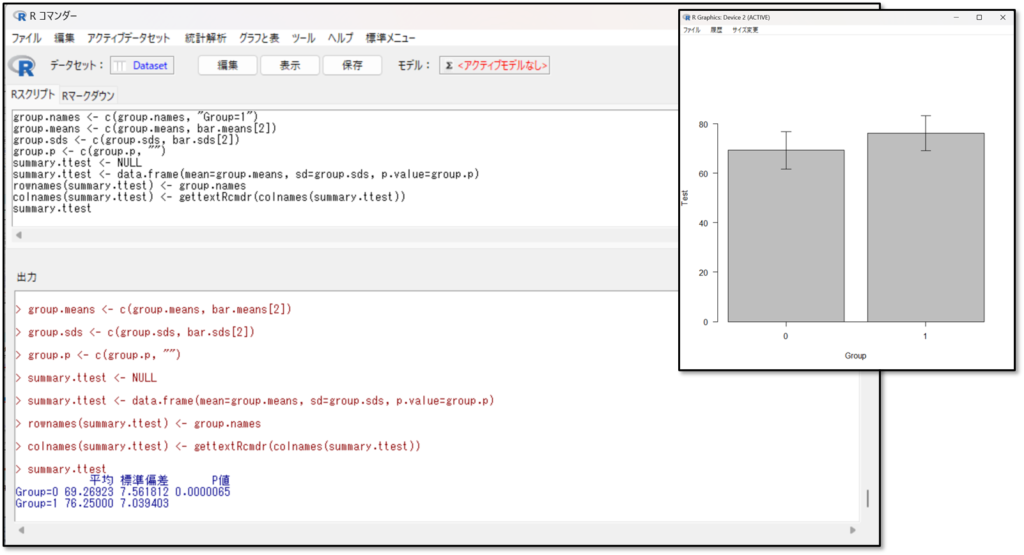
結果の見方は、まずは棒グラフも出力されるので視覚的に2標本の差を確認しましょう。棒グラフの上に出ているのがエラーバーと言います。エラーバーとはデータのばらつきを表します。エラーバーは幅が大きいほど、ばらつきが大きいことを示します。次に「平均値」「標準偏差」で各群の要約したデータを確認します。そして「p値」を確認し、p値がp<0.05であれば、有意な差があると判断します。
改めて今回の結果をみてみましょう。まずは棒グラフです。
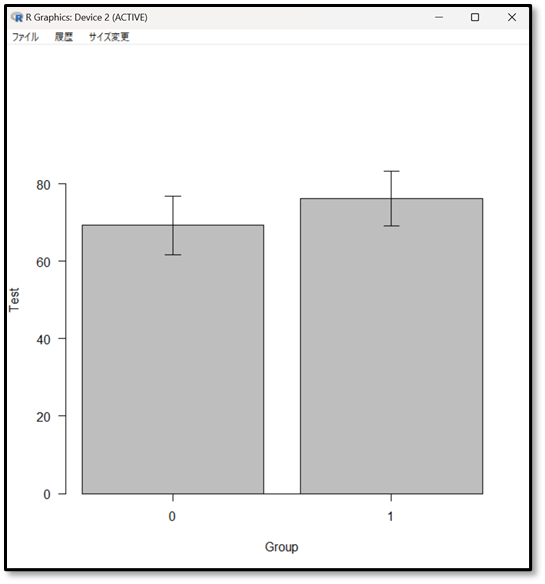
視覚的に、グループB(1)の点数が高そうですね。エラーバーは同じような幅でばらつきもそれほど大きくないですね。棒グラフでみた感じだと、少し差がありそうです。
次に要約したデータとp値を見てみましょう。

グループA(0)は平均69点くらい、標準偏差が7.5くらいです。グループB(1)は平均点が76点くらいで標準偏差が7くらい。P値を見ると、0.000000065なのでpが0.05以上で有意な差があるという結果です。
等分散していなかった場合は?
もし等分散の確認でp値が0.05未満で等分散していなかった場合はWelchの修正による2標本t検定を選択します。
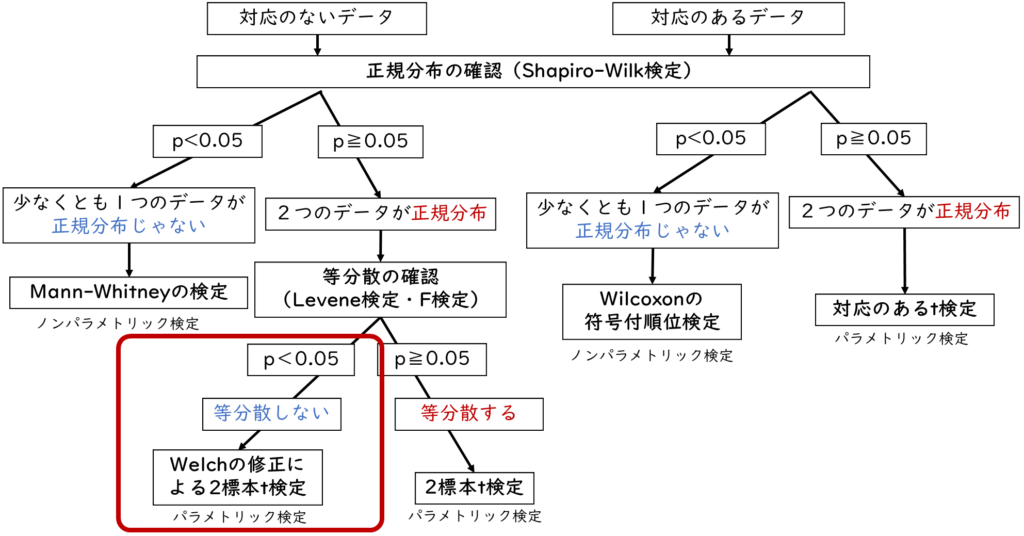
等分散していない場合は、先ほどと同様の手順で2群間の平均値の比較(t検定)を選択します。そして変数選択の際の「等分散と考えますか」の質問にいいえ を選択するとWelchの修正による2標本t検定の算出結果が出力されます。
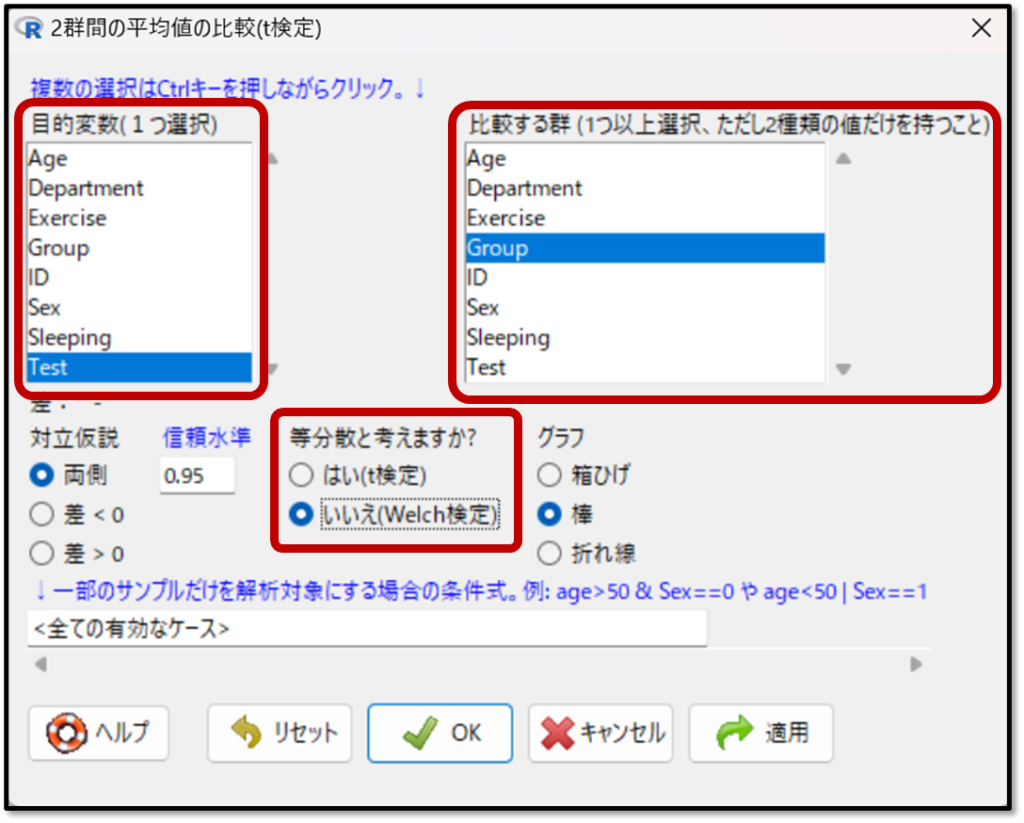
なお、Welchの修正による2標本t検定の場合も、出力内容は先ほどと同様で、結果の解釈も同様です。
2標本の少なくとも1つが正規分布していない場合
次にAグループとBグループの少なくとも1つのデータが正規分布していない場合の対応のない2群の差の検定について解説します。

デモデータの中の「データ2」と記載されたデータが、どちらか一方が正規分布しないように調整したデータだよ。
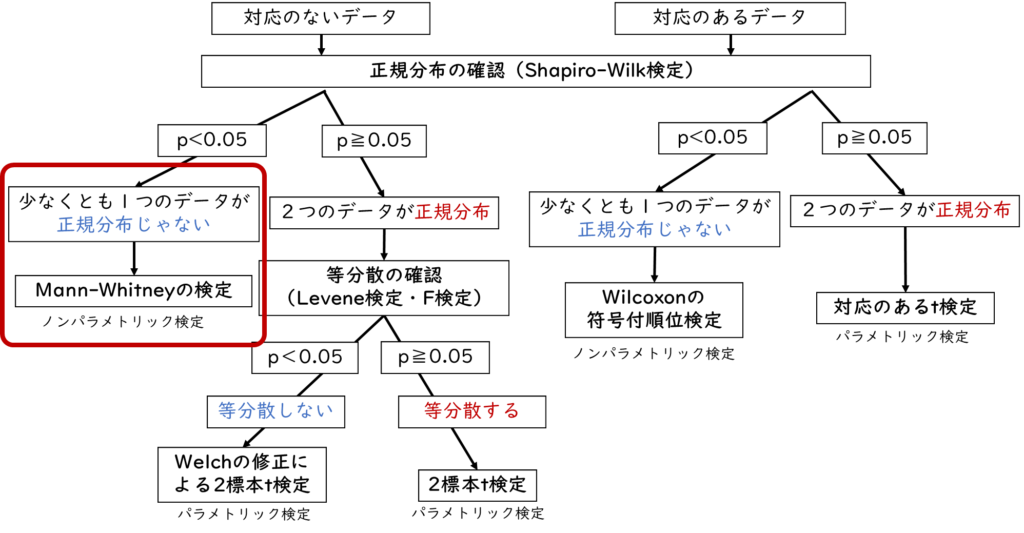
少なくとも1つのデータが正規分布していない場合、Mann-Whitneyの検定を使用します。まずは、「統計解析」→「連続変数の解析」→「2群間の比較(Mann-Whitney U検定)」を選択します。
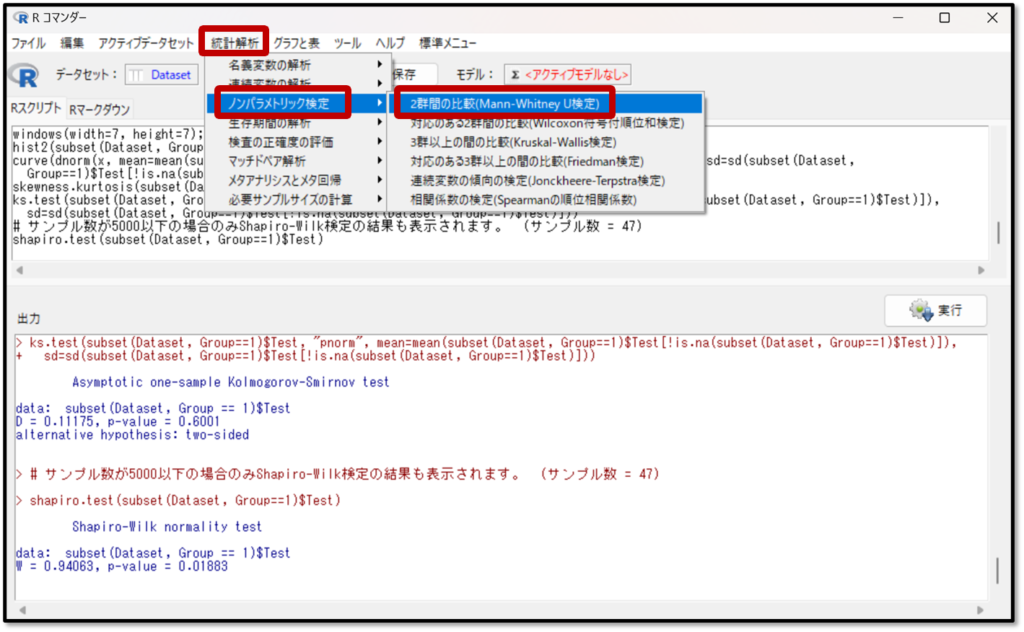
「2群間の比較(Mann-Whitney U検定)」をしたい変数として、目的変数にテスト を選択して比較する群はグループを選択します。
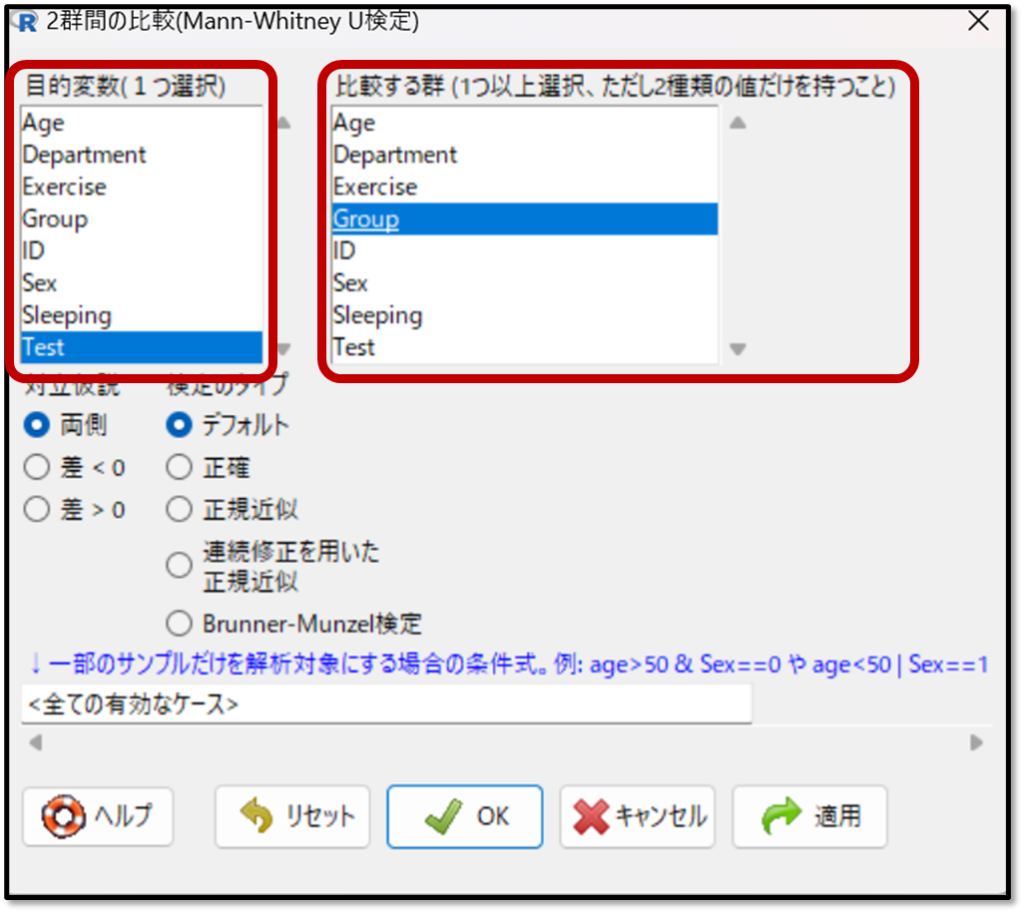
下記が「2群間の比較(Mann-Whitney U検定)」の出力結果です。
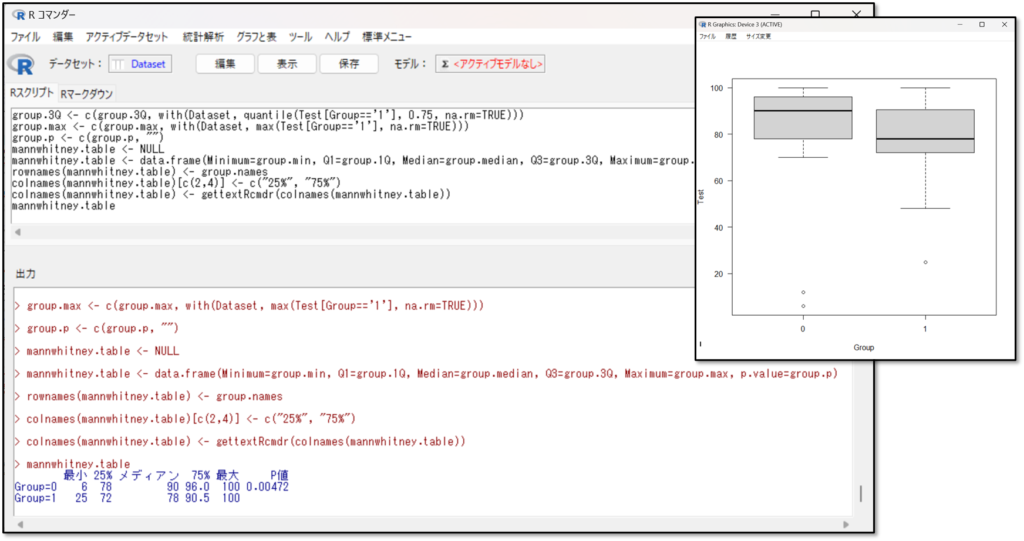
結果の見方は、まずは箱ひげ図が出力されるので視覚的に2標本の差とデータのばらつきを確認します。次に赤枠部分の「メディアン(中央値)」「最小、25%・75% (四分位範囲) 、最大」で各群の要約したデータを確認します。最後に「p値」を確認し、p値がp<0.05であれば、有意な差があると判断します。
それでは改めて今回の出力結果をみてみましょう。まずは箱ひげ図です。
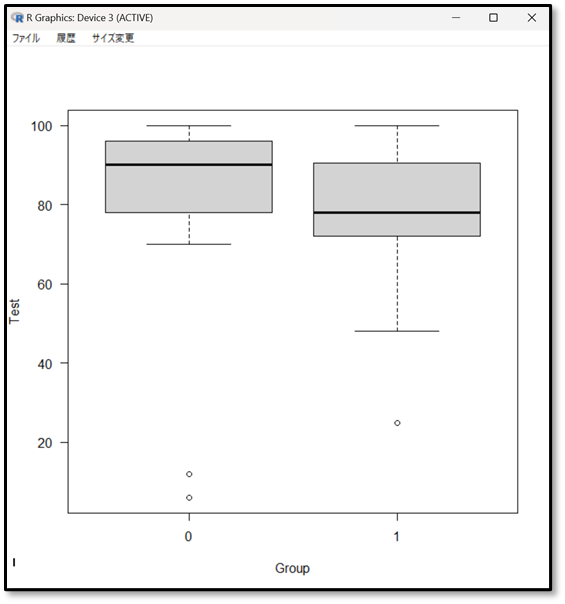
Aグループ(0)の方が点数が高く、2群間で差がありそうですね。中央値も四分位範囲のばらつきも差がありそうです。
次に要約されたデータとp値を見てみましょう。

グループA(0)のテストの点数のメディアン(中央値)は90、ばらつきである四分位範囲は、25パーセンタイル値が78、で75パーセンタイル値が96、グループB(1)のテストの点数のメディアン(中央値)は78、ばらつきである四分位範囲は25パーセンタイル値は72、75パーセンタイル値は90です。どちらも大きな差はないですね。P値は0.00472。pが0.05未満なので、グループAとBのテストの点数には、有意な差があると判断します。
中央値・四分位範囲・箱ひげ図とは?
正規分布に従っていないデータを扱うノンパラメトリック法では、データの代表値は中央値(Median)で示し、データのばらつきは四分位範囲(IQR:Interquartile Range) 、図は箱ひげ図で表します。

正規分布(パラメトリック)の場合は、データを代表する値として平均値を確認し、ばらつきは標準偏差で確認します。
中央値・四分位範囲とは?
まずは中央値について解説します。中央値とは、データを大きさの順に並べた時の中央の値のことです。また四分位範囲とは、データを大きさの順に並べて4等分したもので、データのばらつきを表します。
下記の図で25%から75%の範囲を四分位範囲と呼び、データのばらつきを表します。

論文では中央値(四分位範囲)と記載します。四分位範囲は25%点-75%点の範囲でしたので、中央値は50%値(25%値-75%値)を記載します。
また、「最小値」と「最大値」の範囲で記載することもあり、この場合は「 Range」と呼ばれます。「Range」は(0%値-100%値)を記載します。
次に箱ひげ図について解説します。箱ひげ図とは四分位数(大きい順に並べて、パーセント表示したもの)を用いてデータの散らばりを表した下記のような図のことです。
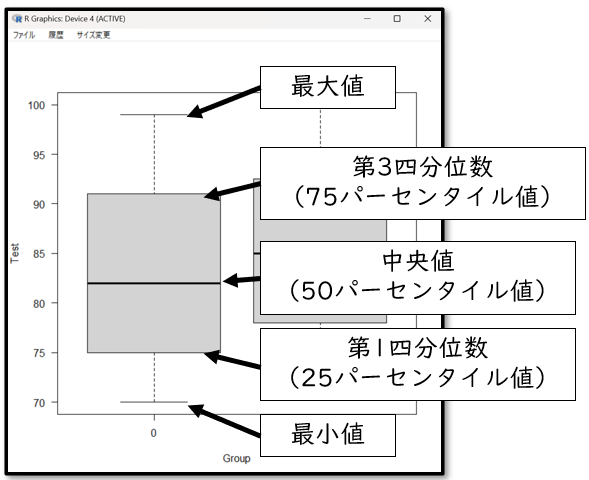
一番上の線、ひげの一番上は最大値です。ここは90パーセンタイル値を用いる場合もあります。
次に長方形の一番上の返が第3四分位数(75パーセンタイル値)つまり、大きい順に並べて75%の値、長方形の真ん中が、中央値(50パーセンタイル値)、大きい順に並べて真ん中の値です。
そして長方形の下の返が第1四分位数(25パーセンタイル値)、大きい順に並べて25%の値、そして最後に一番下の線、ひげの一番下が最小値です。ここは10パーセンタイル値を使用することもあります。

ちなみにパーセンタイル値とは、四分位数でパーセント表示した際に使用する用語だよ。
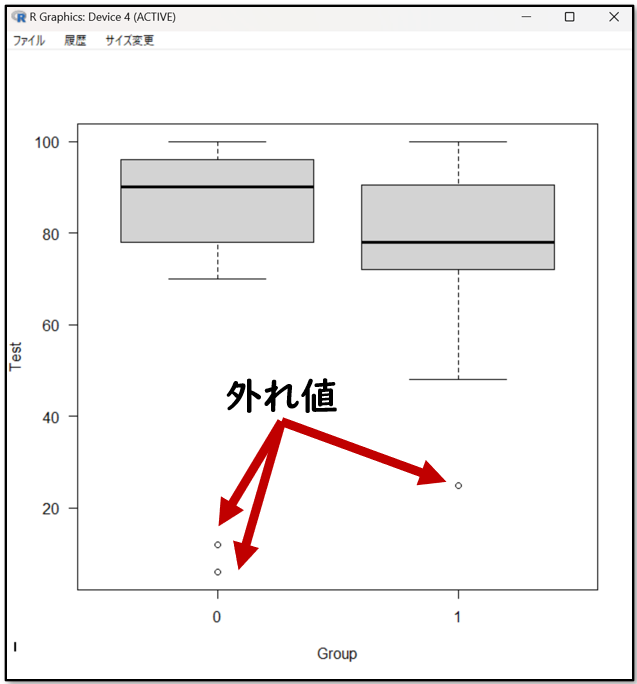
「箱ひげ図」を分析する際は「外れ値」を確認する
「外れ値」の取り扱いが重要となるため必ず確認しましょう。
外れ値とは、データの分布において、他の観測値から大きく外れた値のことです。つまり「他と比べて極端に小さな値、あるいは極端に大きな値」のことです。外れ値の原因には測定ミスや入力ミスなどがあります。
しかし、「外れ値」は何か意味を持つ値の可能性もあります。そのため、外れ値がある場合は、統計学的な意味以外でも分析が必要です。
先ほどの分析結果の箱ひげ図にも、下記にように外れ値が示されていました。グラフの下にある点が外れ値です。全体の値よりも、大きく外れていることが分かります。
まとめ

本記事が対応のないデータ分析の基礎となる2標本の差の検定の理解に役立つことを願っています。対応のない2標本の差の検定は、医学研究から市場調査、教育の効果評価に至るまで、幅広い分野での応用が可能です。EZRを活用することで、これらの統計手法をより深く理解し、実際のデータ分析に応用する能力を養うことができるでしょう。

あなたの研究結果がさらなる知識の発展と社会への貢献につながることを期待しています!
今回は2標本の差の検定(“対応のない”データ)を実際に行う方法を解説しました。2標本の差の検定の概要を知りたい方は下記を参照してください。











コメント