Last Updated on 2025年2月17日 by カメさん

こんにちは!看護師のカメさん(@49_kame)です。
この記事は10分程度で読めます。

今回は統計解析ソフトEZRを使用して実際に分散分析・多重比較(対応のあるデータ)を行う方法を解説します。対応のあるデータとは時間経過に伴うデータなどのことだよ。
看護研究は、医療現場での実践が科学的根拠に基づいていることを確かめるために不可欠な役割を担っています。データ分析はこのプロセスの核となる部分であり、看護師や研究者が患者ケアの質を高めるための介入が実際に効果があるかどうかを判断するために使われます。特に、分散分析(ANOVA)と多重比較法は、異なる治療法や看護介入の効果を比較し、その有効性を検証する上で欠かせない統計的手法です。これらの方法を用いることで、研究者は偶然による結果の違いではなく、実際の効果に基づいて結論を導くことができます。
しかし、これらの統計的分析手法は多くの初学者にとって難解であり、理解するためには専門的な知識が求められます。この記事では、分散分析と多重比較法を、デモデータを使用しながら初学者でも理解しやすいように丁寧に説明していきます。

この記事を通じて、看護研究における統計分析の基礎知識を身につけ、実際の研究でこれらの手法を効果的に活用するための一歩を踏み出すことができれば幸いです!
このブログでは統計解析ソフトしてEZRを使用しています。EZRは無料かつ精度も高い統計解析ソフトであるためおすすめです。EZRの概要とインストール方法については【EZRの概要とインストール方法】看護研究を変える!EZRで効率的な統計解析を参照してください。
はじめに

まずは分散分析の概要から解説するよ。分散分析の実践編➀で解説した内容と重複するから、具体的な検定方法を知りたい人は「EZRで行う分散分析・多重比較法の検定手順(“対応のない”データ)」から参照してね。
分散分析とは?
分散分析(ANOVA)は、3つ以上のデータ間で平均値に差があるかどうかを検証する統計手法です。平均値の比較において、複数のサンプル群間での差を一度に検討できるため、効率的な方法とされています。ただし分散分析では、「どこかのグループ間に差があるだろう」ということだけが分かります。さらに詳細な分析は多重比較法を実施します。

多重比較法とは?
多重比較法は、群間の差を個別に検討する手法です。分散分析で群間に差があると判断された場合、どの群が他と異なるのかを特定するために使用されます。つまり分散分析の結果、グループの間のどこかに差があることが分かったら、どのグループ間に差があるかを、多重比較法で判定します。

分散分析や多重比較法の概要を知りたい方は【分散分析:概要編➀】看護研究の疑問を解決「3つ以上の”対応のない”データを分析しよう」・【分散分析:概要編②】看護研究の疑問を解決「3つ以上の”対応のある”データを分析しよう」を参照してください。
対応のないデータと対応のあるデータとは?
対応のないデータとは、互いに独立したグループ間で比較が行われる場合です。また対応のあるデータは、同じ被験者が異なる条件下(同一人物の前後テストなど)で測定されたデータなどを指します。
対応のあるデータの分散分析とは?
対応があるデータを用いた分散分析とは、1つのグループから収集する3つ以上のデータを比較する分析のことです
例えば、1グループへの介入前後、1カ月後の点数の比較などです
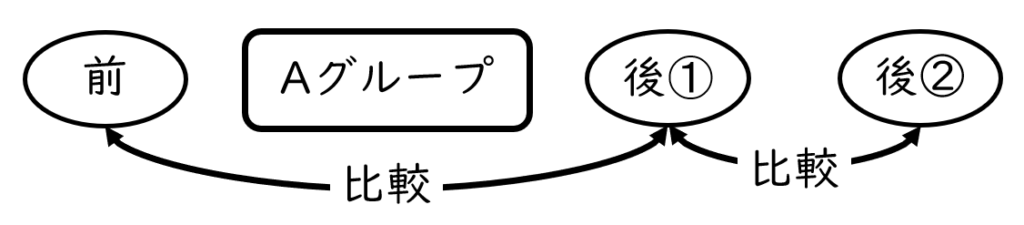
分散分析・多重比較法の基本的な流れ
下記が基本的な分散分析・多重比較法の流れになります。
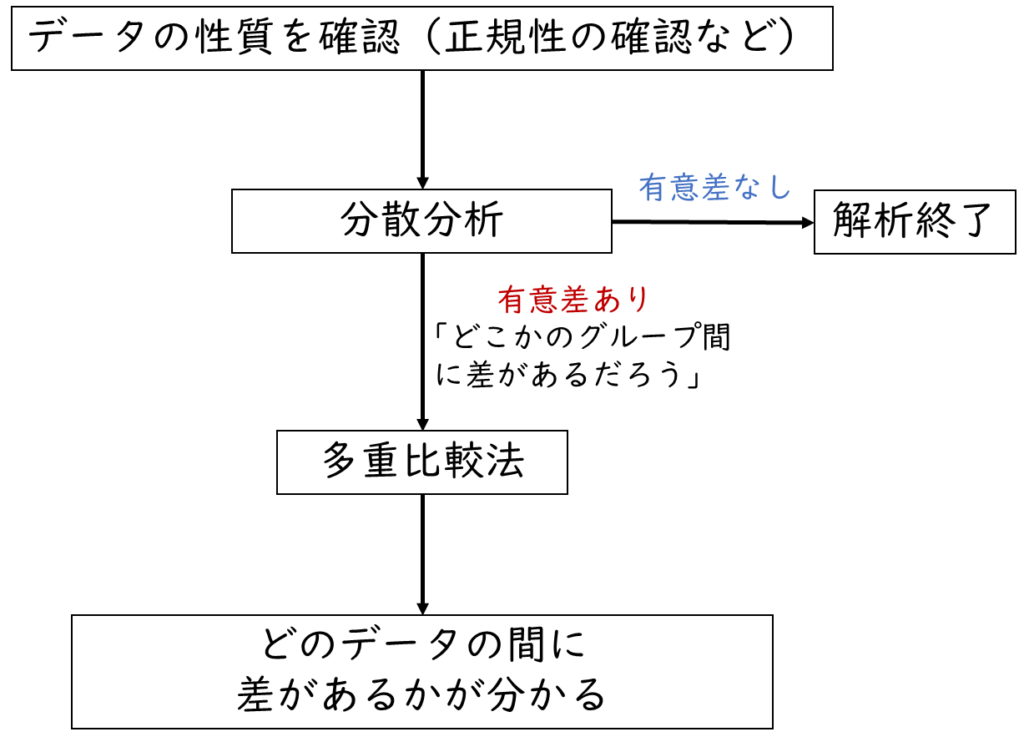
まずはデータの性質(正規分布かどうかなど)を確認し、その上で分散分析を行います。分散分析が有意でなければその時点で解析終了となります。
もし分散分析の結果が有意であれば、どこかのグループ間に差があることが分かります。そのため、どこのグループ間に差があるかを調べるために多重比較法を行います。多重比較法を行うことで、どのグループとどのグループの間に差があるかが分かります。

分散分析で、差があるかどうかを簡単に確認して、どこかに差があるのであれば、多重比較法で詳細に分析するイメージだね。
分散分析・多重比較法には種類がある
分散分析・多重比較法には、他の統計解析方法と同様に種類があります。解析方法の種類の選択にはデータの種類(対応あるデータ or 対応のないデータ)、正規性、等分散性などの前提条件を確認する必要があります。これらの条件に応じて適切な手法を選択します。
分散分析・多重比較法は以下の4つのポイントで決まります。
- ➀「対応のあるデータ」か 「対応のないデータ」
- ②「正規分布」 か「正規分布でない」
- ③「等分散する」か 「等分散しない」
- ④「球面性を仮定できる」 か「球面性を仮定できない」
上記のポイントを踏まえた分析方法の早見表が下記になります。セルの中の赤い矢印が多重比較法です
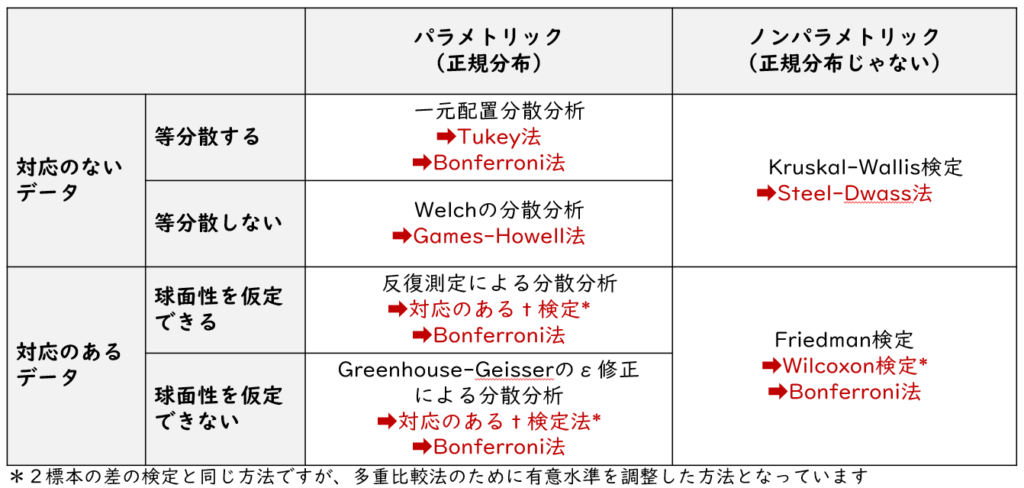

収集したデータの特徴に合わせて分析方法を検討しよう。今回は”対応のある”データに焦点を当てて解説するよ。
EZRで行う分散分析・多重比較法の検定手順(“対応のある”データ)
今回はEZRを使用して「対応のあるデータ」の分散分析・多重比較法について解説します。
今回使用するデモデータ
今回は下記のデモデータ(一部抜粋)を使用します。
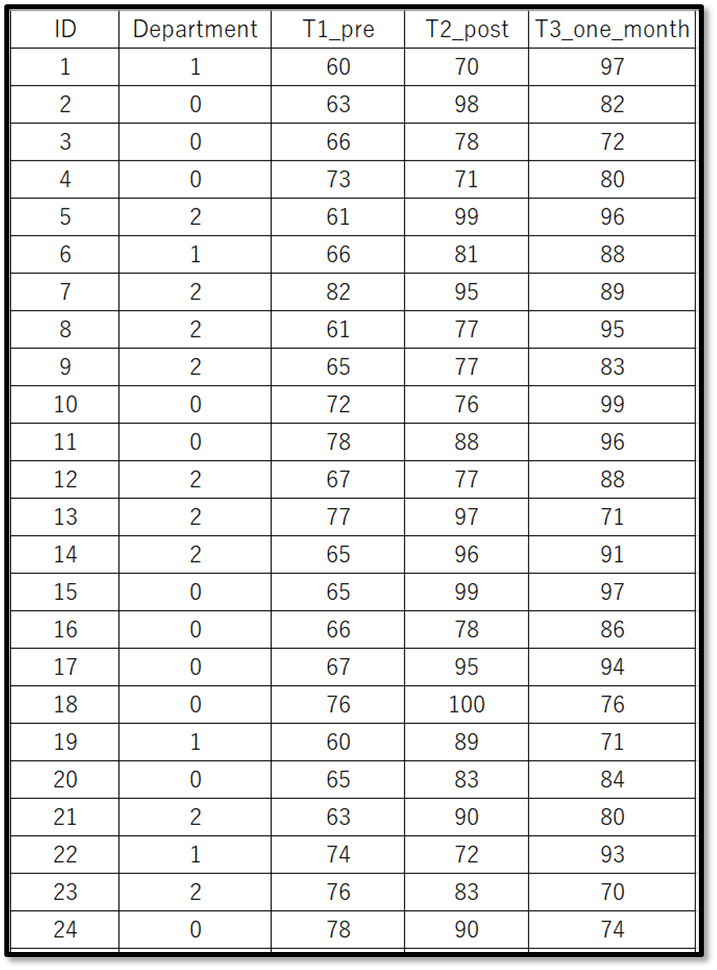
表示しているのは、デモデータの一部です。デモデータは下記からダウンロードできるので使ってみてください。

ランダム関数で作成しているため、今回の結果とズレが出るかもしれませんが、ご了承ください。
こちらのデモデータを読み込んだ後の段階から解説します。データの読み込み方法については、【統計解析ソフトにデータを入力】看護研究初めの一歩:EZRにデータセットを入力しよう!を参照してください。
今回は対応のあるデータとして、ある1つのグループへの介入前後のテスト(プレテストとポストテスト)、介入後1カ月後のテストの3つの点数を比較します。 下記のように、介入前テスト(プレテスト)がT1_pre、介入後テスト(ポストテスト)がT2_post、介入1カ月後のテストがT3_one_monthで表現しています。
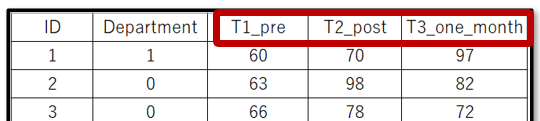
期間を示す変数を設定する場合は、最初にアルファベットを置いて、その後で1、2、3と順序が分かるようにしましょう。そうすることで、統計ソフトに読み込んだ後も、順序立てて計算してくれます。
「対応のあるデータ」の分散分析・多重比較法の検定手順
下記が対応のあるデータについての分散分析・多重比較法の手順です。下記の手順に従って解説していきたいと思います。
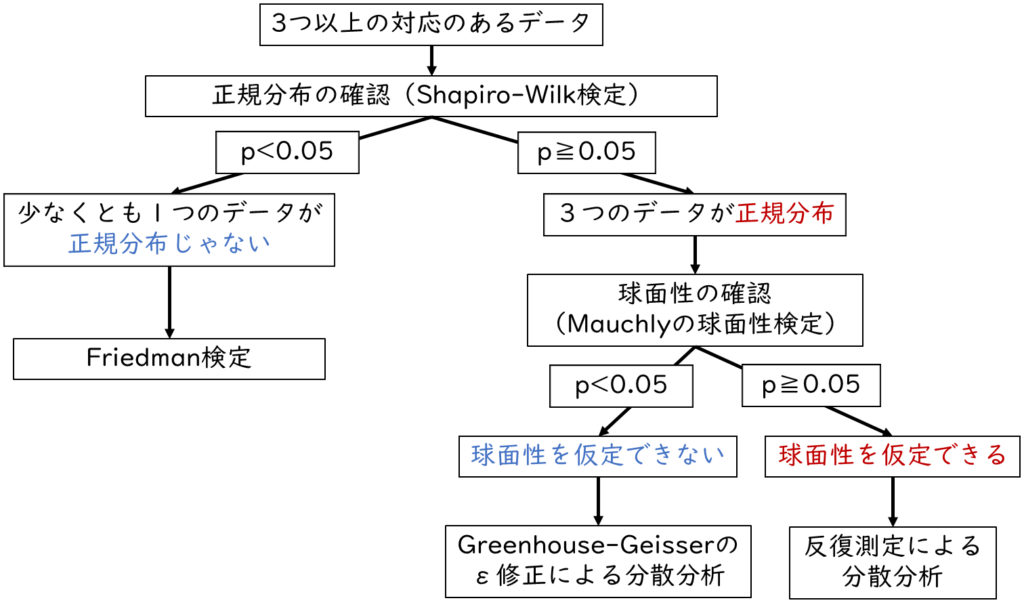
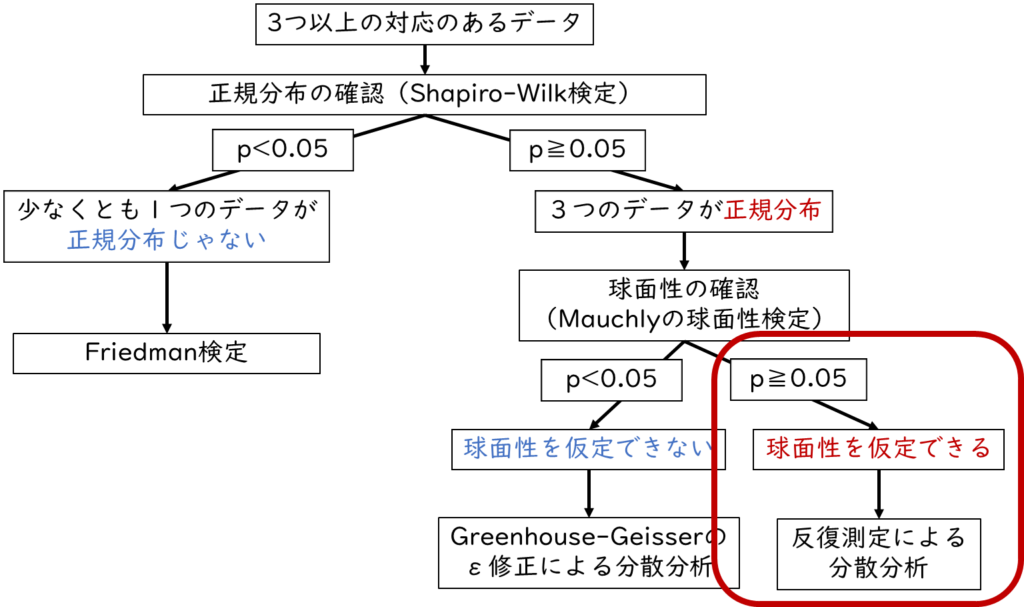
まずは介入前後のテスト(プレテストとポストテスト)、介入後1カ月後のテストの3つの点数についてそれぞれ正規分布を確認します。今回は正規分布の確認手順は割愛します。詳しく知りたい方は【正規分布とは?:実践編】看護研究の疑問を解決「EZRで正規分布を確認しよう」を参照してください。
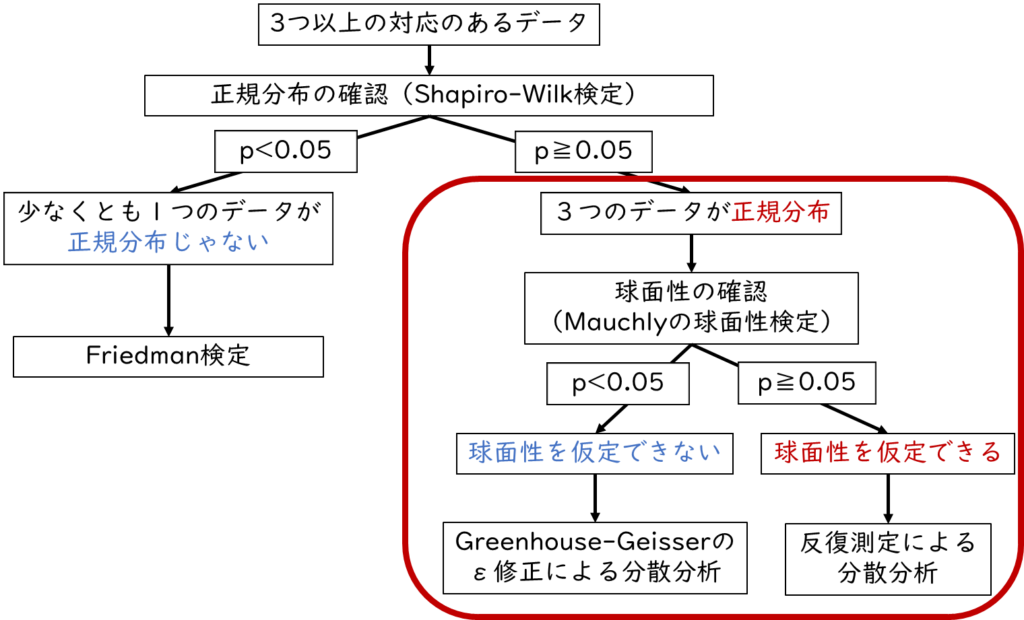
3つのデータが正規分布している場合
3つのデータがどれも正規分布している場合、次は球面性の確認を行います。そして、球面性の確認を行った上で、Greenhouse-Geisserのε修正(グリーンハウス・ガイザーのイプシロン修正)による分散分析もしくは反復測定による分散分析を行います。
ただしEZRでは、球面性の確認(Mauchlyの球面性の検定)の結果とGreenhouse-Geisserのε修正(グリーンハウス・ガイザーのイプシロン修正)による分散分析もしくは反復測定による分散分析の結果が同時に算出されます。そのためMauchly(マーキュリー)の球面性の検定の結果を確認して、どちらの分析方法の結果を採用するかを判断しましょう。

デモデータの中の「データ1」と記載されたデータが3つのデータがどれも正規分布になるように調整したデータだよ。
それでは解析を行っていきましょう。EZRの操作画面で「統計解析」→「連続変数の解析」→「対応のある2群以上の間の平均値の比較(反復【経時】測定分散分析)」を選択します。
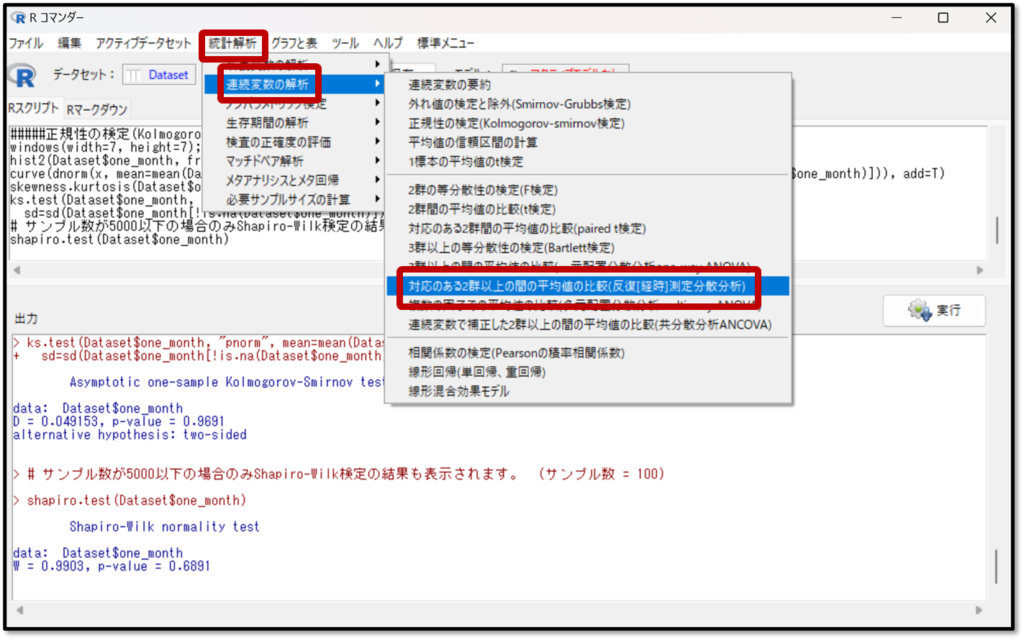
次に下記の画面で、平均値の比較をしたい変数を選択します。今回は、介入前(T1_pre)、介入直後(T2_post)、介入1カ月後(T3_one_month)のデータを選択します。
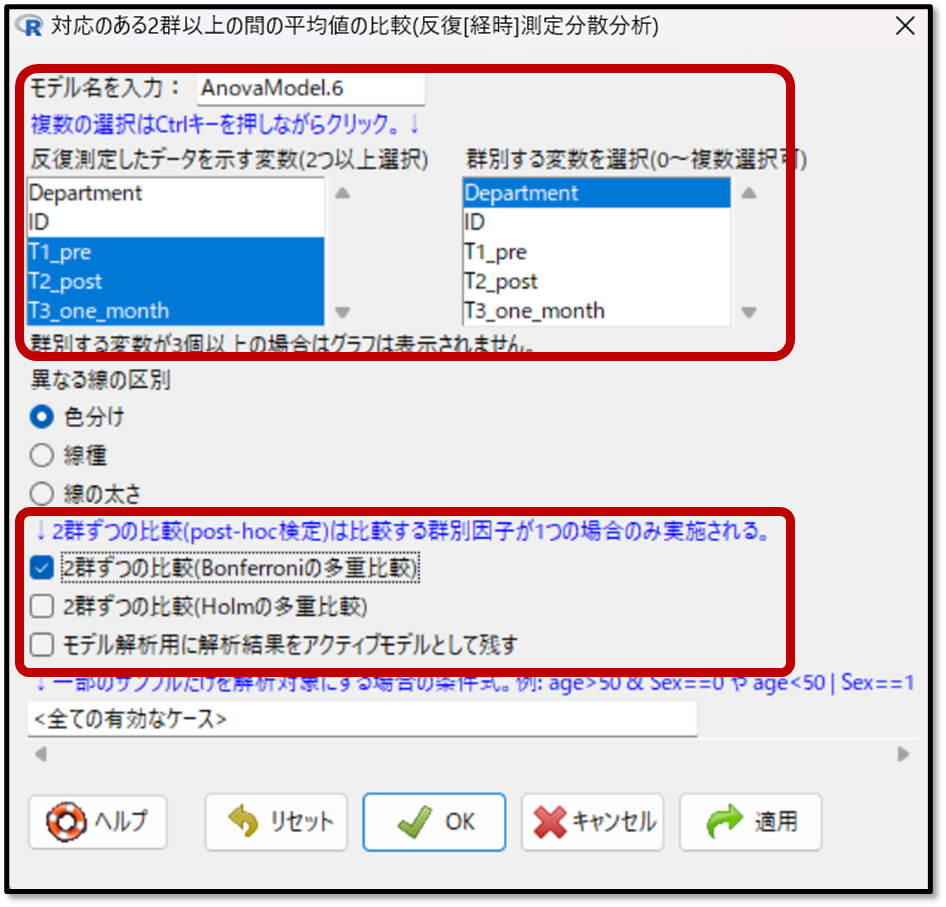
ちなみに、群別する変数を選択することで、群毎(グループ毎)のデータの変化も算出することができます。例えば今回だと、Departmentを選択することで、所属部署毎の、介入前・介入直後・介入1カ月後のデータの変化を確認することができます。
またEZRでは多重比較の方法も、上記の変数選択の段階で決定します。
今回は3つのデータが正規分布しているので、分散分析の方法はGreenhouse-Geisserのε修正(グリーンハウス・ガイザーのイプシロン修正)による分散分析もしくは反復測定による分散分析となります。そのため、使用する多重比較法は対応のあるt検定もしくはBonferroni(ボンフェローニ)法となります
EZRにはBonferroni(ボンフェローニ)法があるので、使用する多重比較法として、Bonferroni(ボンフェローニ)法を選択しましょう
下記が出力結果です。図(グラフ)と数値にて出力されます。
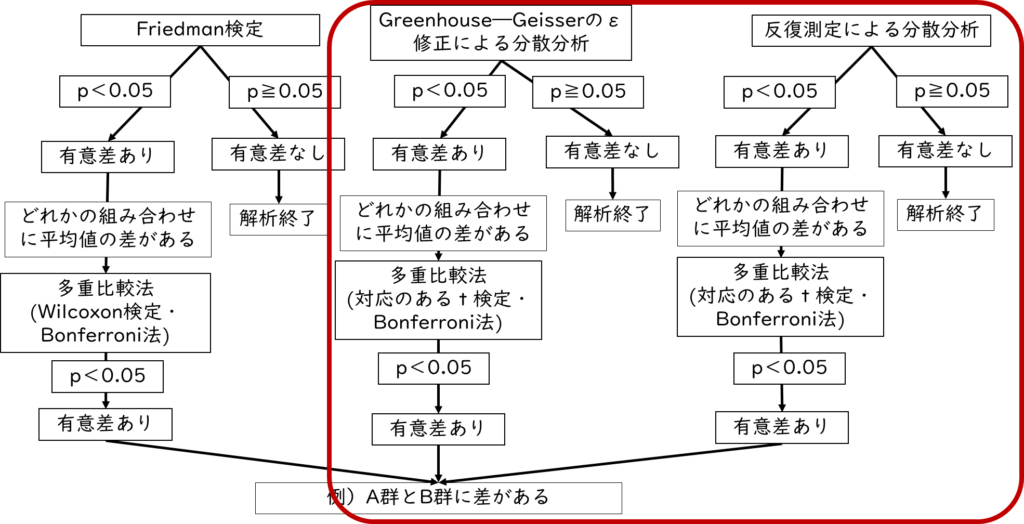
まずはMauchly(マーキュリー)の球面性の検定の結果から球面性を確認します。p値(p-value)を確認し、p<0.05であれば「球面性を仮定できない」、p≧0.05であれば「球面性を仮定できる」と判断します。「球面性を仮定できない」場合は、Greenhouse-Geisserのε修正(グリーンハウス・ガイザーのイプシロン修正)による分散分析を選択します。また、p値が0.05以上で「球面性を仮定できる」場合は、反復測定による分散分析を選択します。
下記がMauchly(マーキュリー)の球面性の検定の結果です。

p値(p-value)は0.62992で、p値が0.05以上だったので、「球面性を仮定できる」と判断します。そのため反復測定による分散分析の結果を確認します。
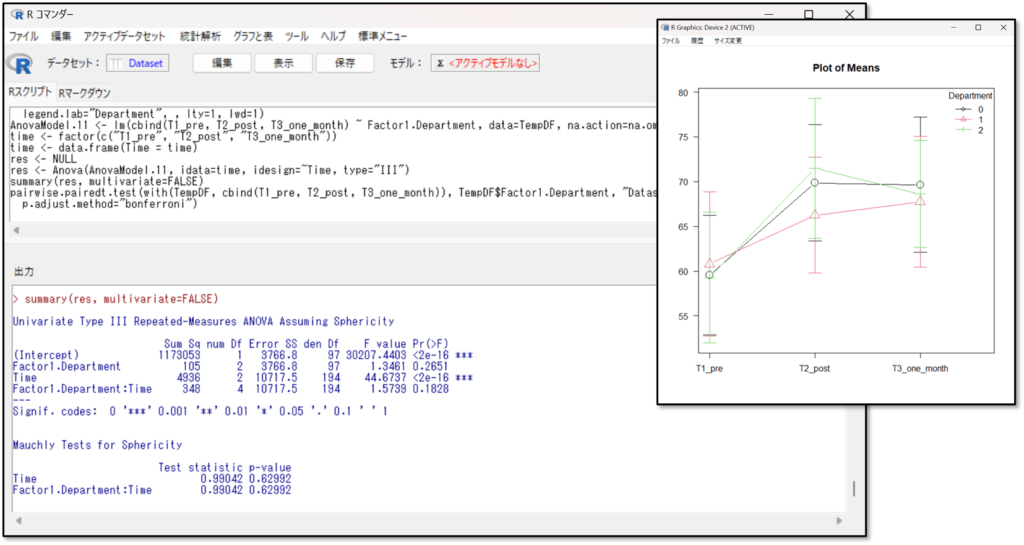
EZRではGreenhouse-Geisserのε修正(グリーンハウス・ガイザーのイプシロン修正)による分散分析と反復測定による分散分析の結果が同時に算出されています。今回は、「球面性を仮定できる」データのため、反復測定による分散分析の結果を確認します。
反復測定による分散分析の結果は、Repeated-Measures ANOVA(反復測定分散分析)の「pr(F)」を確認します。これはp値のことです。p<0.05であれば、3群のどこかに有意な差があると判断します。そのため、多重比較法の結果を確認します。p≧0.05であれば、3群のどこにも有意な差はないので解析終了となります。
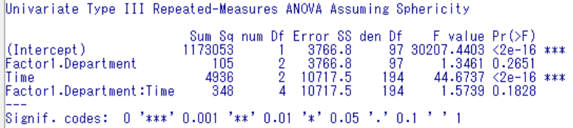
今回は、p値が2e(ネイピア数)-16、つまり2×10-16乗なので、0.000000000002となります。そのため、3群のどこかに有意差があると判断します

p値にイーのような文字が記載されているのは「ネイピア数」と呼ばれるものだよ。「〇e-△」は、〇×10の-△乗を表すよ。ネイピア数があるときは、その数値がかなり小さいことが分かるよ。
図も出力されているので視覚的に3つのデータ間で差があるかどうかも確認しましょう。
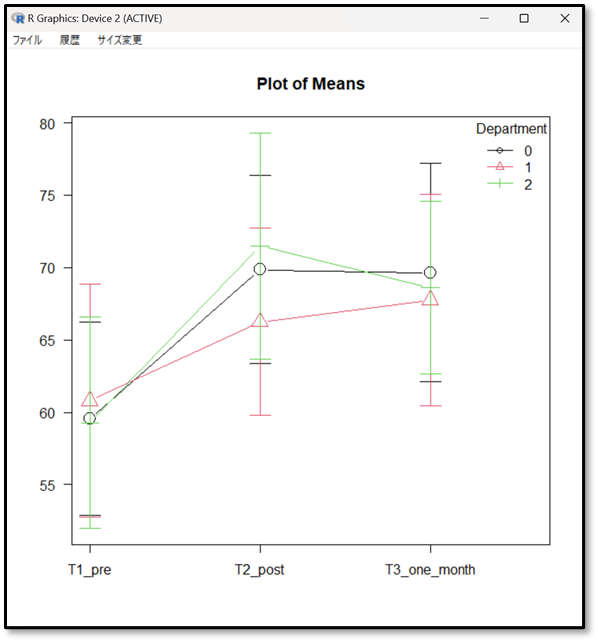
グラフ上でも、3群のどこかに差があるであろうことが分かります。

前述の通り、変数名にT1, T2のように順序性を設定しないと、上手く時系列で計算されないから注意してね!
もし「球面性を仮定できない」場合は?
「球面性を仮定できない場合」は、Greenhouse-Geisserのε修正(グリーンハウス・ガイザーのイプシロン修正)による分散分析の結果を確認します。

分析結果は、さきほどの分析の際に同時に出力されています。
Greenhouse-Geisserのε修正(グリーンハウス・ガイザーのイプシロン修正)による分散分析の結果は、反復測定による分散分析と同様に「pr(F)」を確認します。これはp値です。p<0.05であれば、3群のどこかに有意な差があると判断します。そのため、多重比較法の結果を確認します。p≧0.05であれば、3群のどこにも有意な差はないので解析終了となります。
それでは結果を見てみましょう。
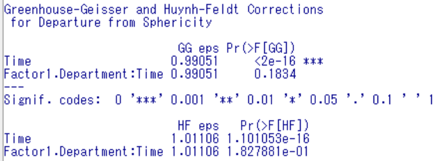
p値はp値が2e(ネイピア数)-16、つまり2×10-16乗なので、0.000000000002となります。そのため、3群のどこかに有意差があると判断します。
分散分析で3群のどこかに有意差があることが分かったので、多重比較法を確認してみましょう。

どこに有意差があるかは気になるところだよね。
今回は、Greenhouse-Geisserのε修正(グリーンハウス・ガイザーのイプシロン修正)による分散分析もしくは反復測定による分散分析なので、多重比較法としてBonferroni(ボンフェローニ)法を選択しました。多重比較法の結果も、先ほどの算出時に同時に出力されているので確認してみましょう。
Bonferroni(ボンフェローニ)法の結果の見方を説明します。Bonferroni(ボンフェローニ)法の結果は縦軸と横軸の表の形式で出力されています。今回だと下記のように縦にポストテスト(T2)・1カ月後(T3)、横軸にプレテスト(T1)・ポストテスト(T2)が並びます。そして、それぞれの組み合わせのp値が記載されています。p値がp<0.05であれば、その組み合わせに有意な差があると判断します。

今回の出力結果を見てみましょう。

今回であれば、左上のT2_post(ポストテスト)とT1_pre(プレテスト)の組みあわせのp値が1.2e(ネイピア数)ー13なので1.2×10の-13乗であり、かなり小さな数値となっています。その下の、T3_one_month(1か月後)と、T1_pre(プレテスト)の組み合わせでも、3.2e(ネイピア数)-11なので、かなり小さな数値であることが分かります。そのため、これらの組み合わせで有意な差があったことが分かります。

“対応のある”分散分析・多重比較法の場合は、パラメトリック法(正規分布のデータ)でも、データの要約が、別操作で必要となるよ。データの要約とは平均や標準偏差などです。下記で簡単に説明するね。
EZRでデータを要約する方法
EZRでデータを要約する操作は他の解析の時と同様です。EZRの画面から「統計解析」→「連続変数の解析」→「連続変数の要約」を選択します。
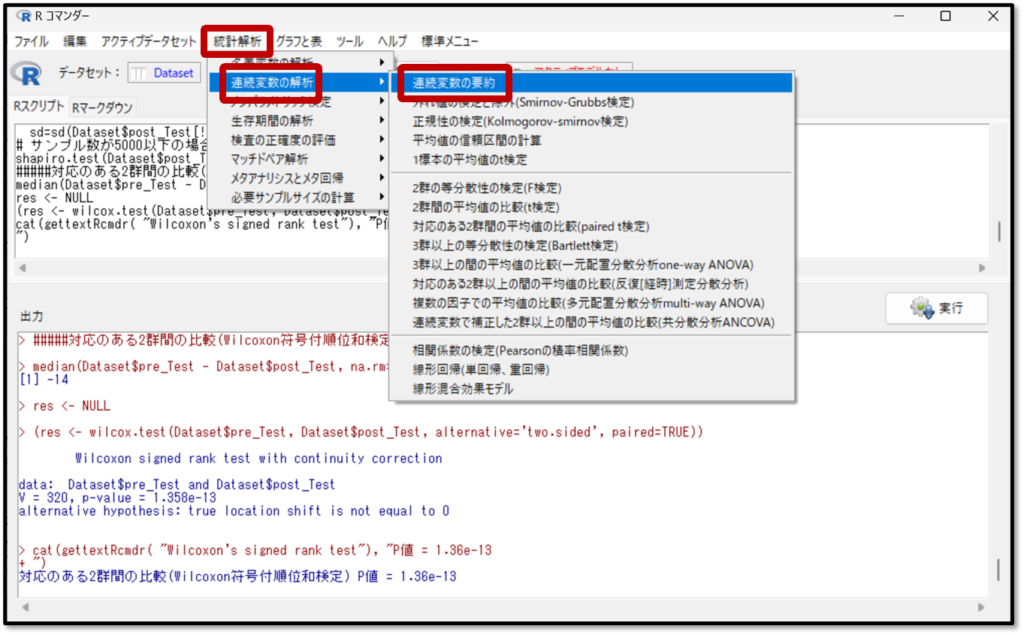
要約したい変数としてT1_pre(プレテスト)とT2_post(ポストテスト)、T3_one_month(1カ月後)のテスト結果を選択します。今回はパラメトリック検定の結果を確認するので平均や標準偏差に✓が入っていればOKです。
下記が、先ほどのデータを要約した出力結果です。
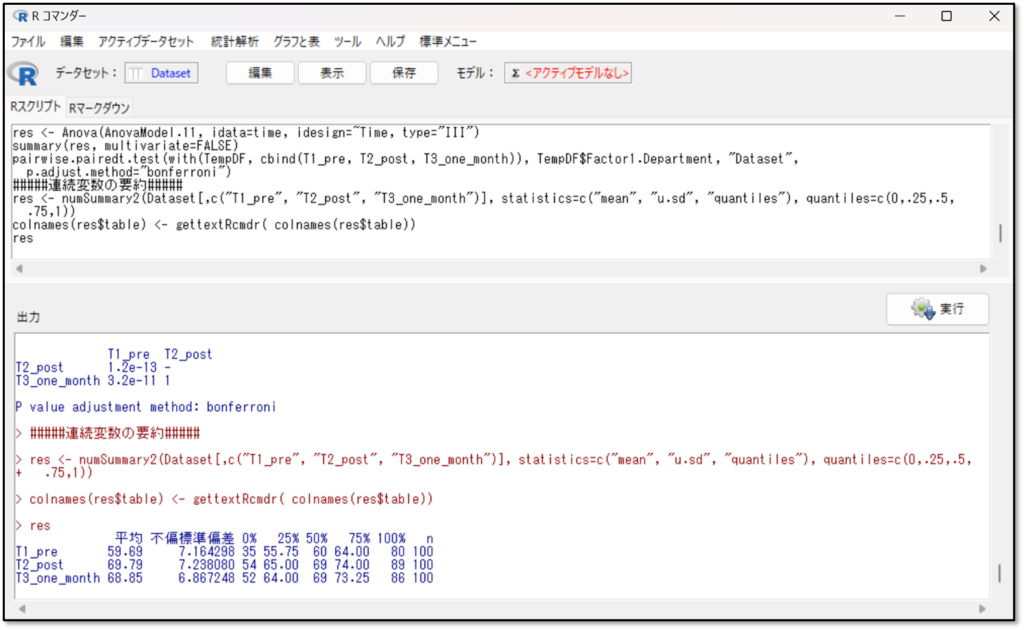
一般的な要約したデータの結果の見方を解説します。
正規分布に従うデータを扱うパラメトリック検定の場合、代表値は「平均」を、データのばらつきは「標準偏差」を確認します。また、正規分布に従わないデータを扱うノンパラメトリック検定の場合は、代表値は「中央値(50%) 」、データのばらつきは「四分位範囲」を確認します。
今回は正規分布に従うデータを扱うパラメトリック検定なので、平均と標準偏差を確認しましょう。

例えば、T1_pre(介入前のプレテスト)のデータの要約を見ると、平均が59.69点、標準偏差が±7.16程度であることが分かります。
層別(グループ分け)したデータの要約もできる
データの要約では層別したデータの要約も確認できます。層別とはグループ分けのことで、今回であれば所属部署毎のテスト結果などを確認することができます。
下記のように層別変数としてDepartmentを選択すると、事前に収集した所属部署毎のデータの要約が出力されます。
下記が、層別したデータを要約した出力結果です。所属部署毎の結果が出力されています。
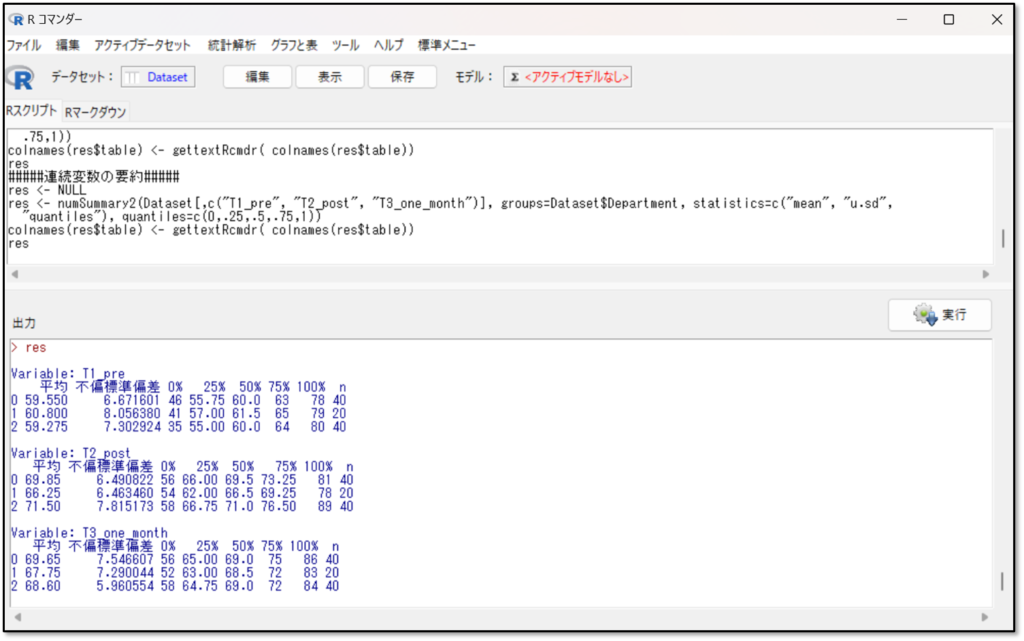
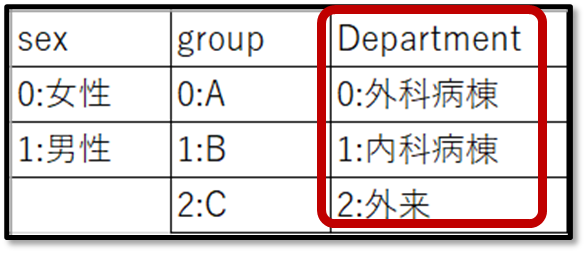
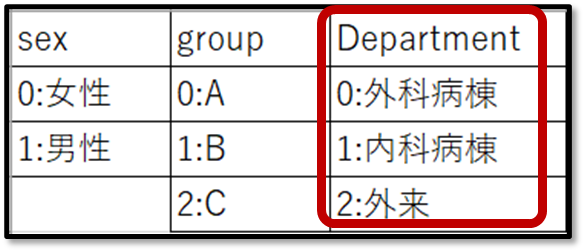
例えば一番上の「Variable:T1_pre」とは、介入前のプレテストの結果です。左に0 1 2というのが、それぞれ事前に下記のようにコード化した0(外科病棟)、1(内科病棟)、2(外来)を示しています。そして、それぞれの点数のデータの要約が表示されています。

これがコード化した内容だよ。
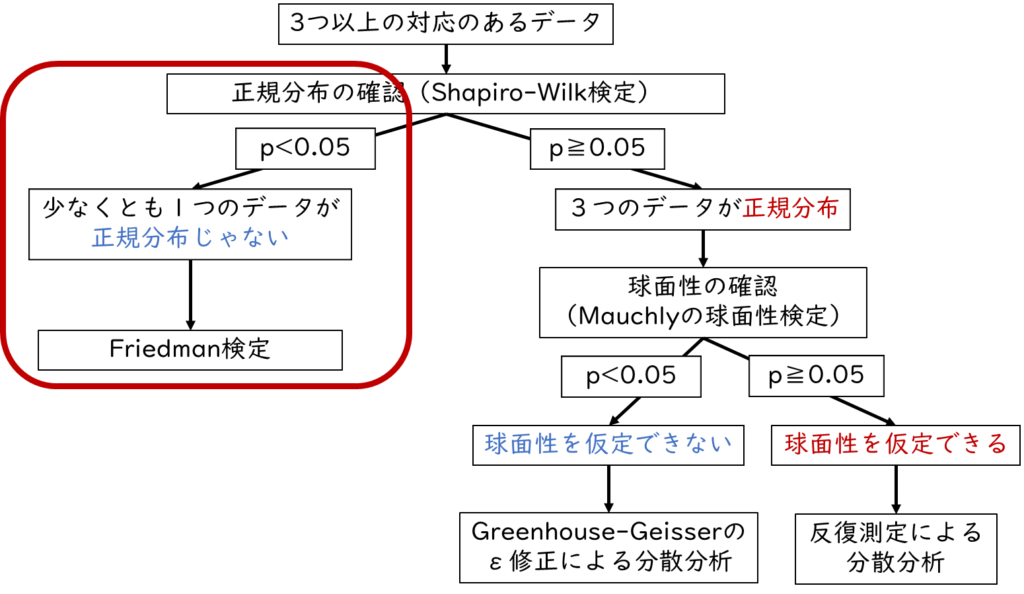
少なくとも1つのデータが正規分布していない場合
続いて、3つのデータのうち少なくとも1つのデータが正規分布していない場合の分散分析についてみて行きましょう。少なくとも1つのデータが正規分布していない場合は、Friedman(フリードマン)検定を行います。

デモデータの中の「データ2」と記載されたデータが少なくとも1つのデータが正規分布にならないように調整したデータだよ。
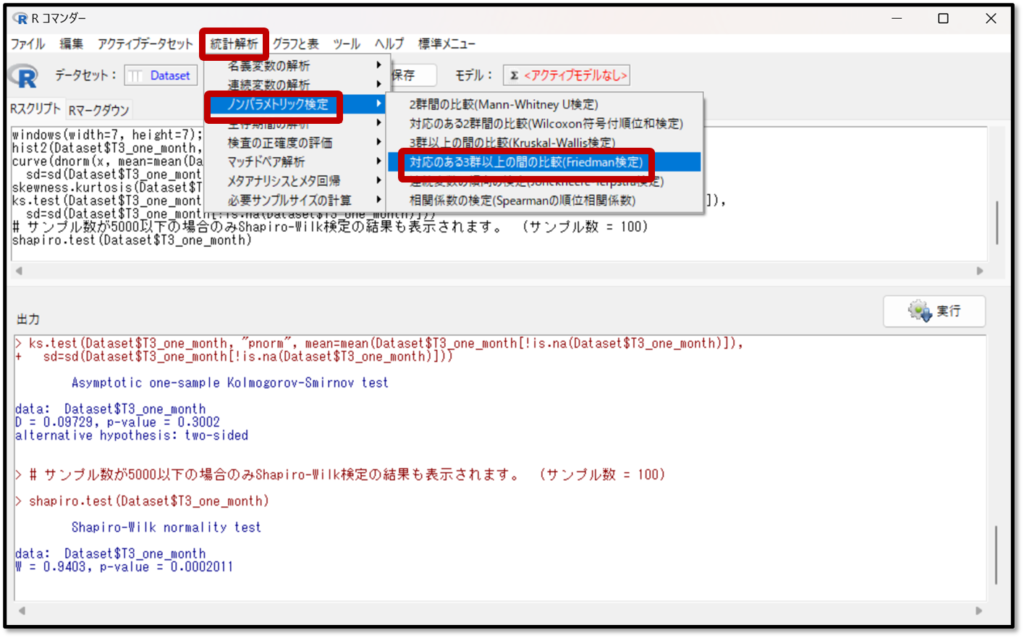
それでは実際の解析手順を解説していきます。EZRの操作画面で「統計解析」→「連続変数の解析」→「対応のある3群以上の間の比較(Friedman検定)」を選択します。
続いてFriedman(フリードマン)検定を行いたい変数を選択しましょう。また、今までと同様にこの時点で多重比較法を選択します。
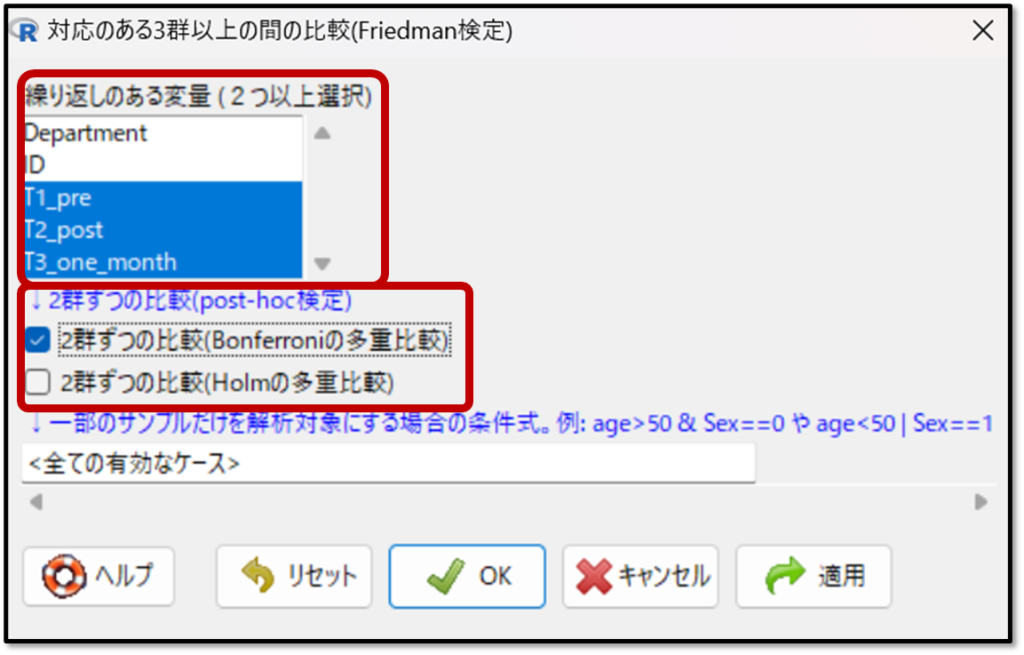
今回はFriedman(フリードマン)検定なので、多重比較法はWilcoxon(ウィルコクソン)検定かBonferroni(ボンフェローニ)法を選択します。
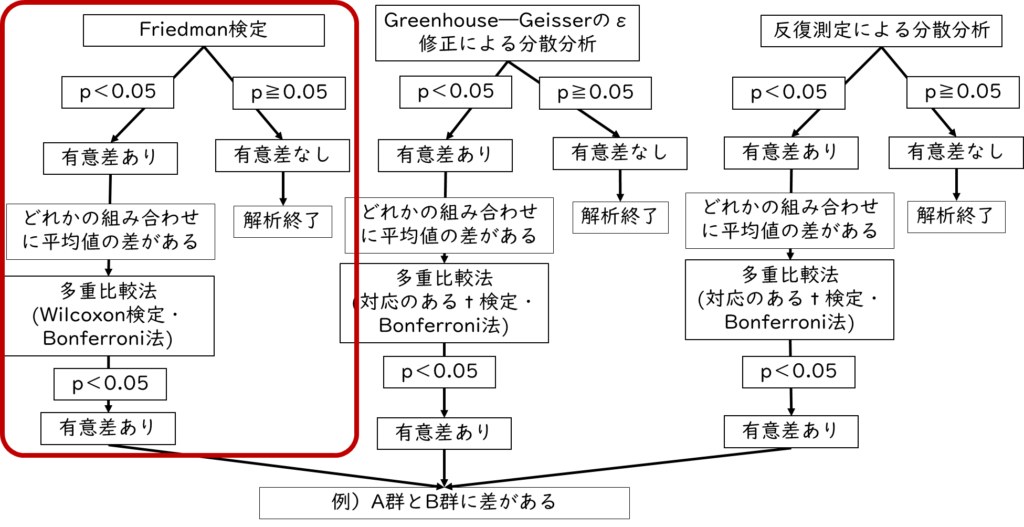
EZRにはBonferroni(ボンフェローニ)法があるのでそちらを選択しましょう。分散分析の結果と同時に多重比較法の結果も出力されます。
下記が分散分析(Friedman検定)の出力結果です。
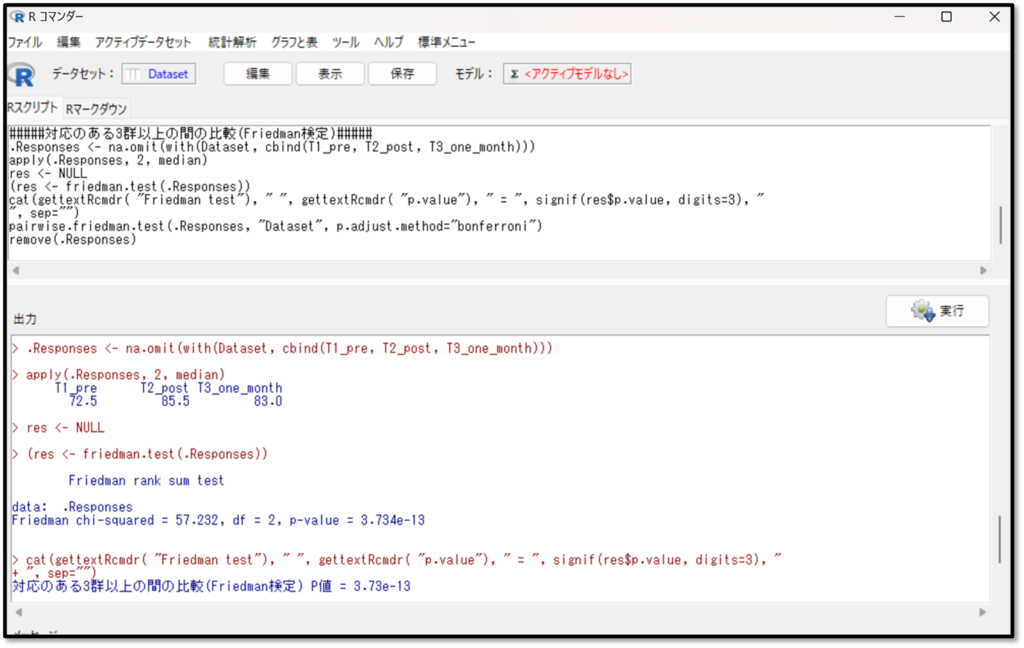
結果の見方を解説します。データの要約として中央値が出力されているので、まずは中央値を確認しましょう。次に「p-value」つまりp値の結果を確認します。p<0.05であれば、3つの群間のどこかに有意な差があると判断します。p≧0.05であれば、有意な差はないと判断し、解析終了となります。

出力されているデータの要約は中央値だけで、四分位範囲については出力されていないよ。
今回の結果を見てみましょう。まずは中央値です。

T1_pre(プレテスト)、T2_post(ポストテスト)、T3_one_month(1カ月後のテスト)の点数の中央値がそれぞれ出力されています。
次にp値を見てみましょう。

今回のp値は3.734e(ネイピア数)-13と出力されました。これは3.734×「10の-13乗」ということです。つまりP=0.0000000000003734であり、3群のどこかに有意な差があることが分かります。分散分析で有意差ありとの結果になったので、続いて多重比較法も見てみましょう
Bonferroni(ボンフェローニ)法の結果の見方を説明します。前述のパラメトリック法(正規分布に従うデータを扱う)の時と同様に、Bonferroni(ボンフェローニ)法の結果は下記のような縦軸と横軸の表でみます。そして群毎の組み合わせのp値がp<0.05であれば、その組み合わせに有意な差があると判断します。

今回の結果を見てみましょう。下記がBonferroni(ボンフェローニ)法の出力結果です。

左上のT2_post(ポストテスト)とT1_pre(プレテスト)のp値が8.1e-14となっています。つまり8.1×「10の-14乗」なのでp値は0.000000000000081であり、有意な差があると判断します。また、その下のT3_one_month(1カ月後のテスト)とT1_preプレテストの組み合わせのp値も2.5e-11となっています。つまり2.5×「10の-11乗」でp値は0.000000000025となり有意な差があると判断します。今回の結果では、この2つの組み合わせに差があったという結果になります。

“対応のあるデータ”の分散分析・多重比較法の場合は、パラメトリック検定ノンパラメトリック検定どちらの場合もデータの要約が、別操作で必要となります。今回の出力結果には中央値は算出されていましたが、ばらつきは分からないので別操作で確認しましょう。
EZRでデータを要約する方法
操作は先ほどのパラメトリック検定(正規分布データを扱う場合)の時と同様です。EZRの画面から「統計解析」→「連続変数の解析」→「連続変数の要約」を選択します。
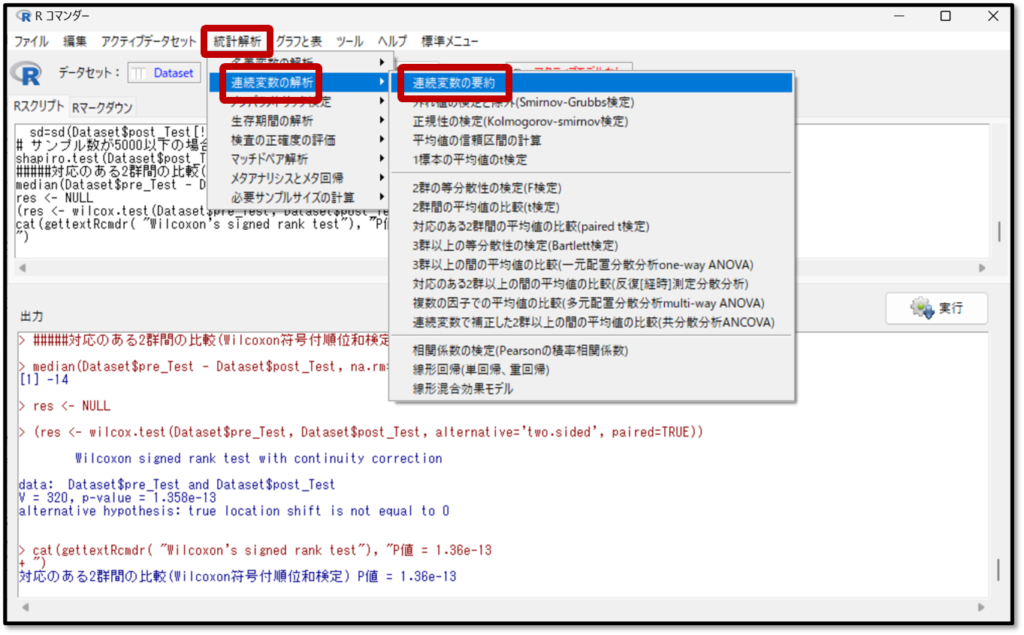
要約したい変数としてT1_pre(プレテスト)とT2_post(ポストテスト)、T3_one_month(1カ月後のテスト)を選択します。平均や標準偏差を確認することもできますが、今回は正規分布していないデータなので、最低でも分位点にだけ✓が入っていれば中央値と四分位範囲を確認できるのでOKです。
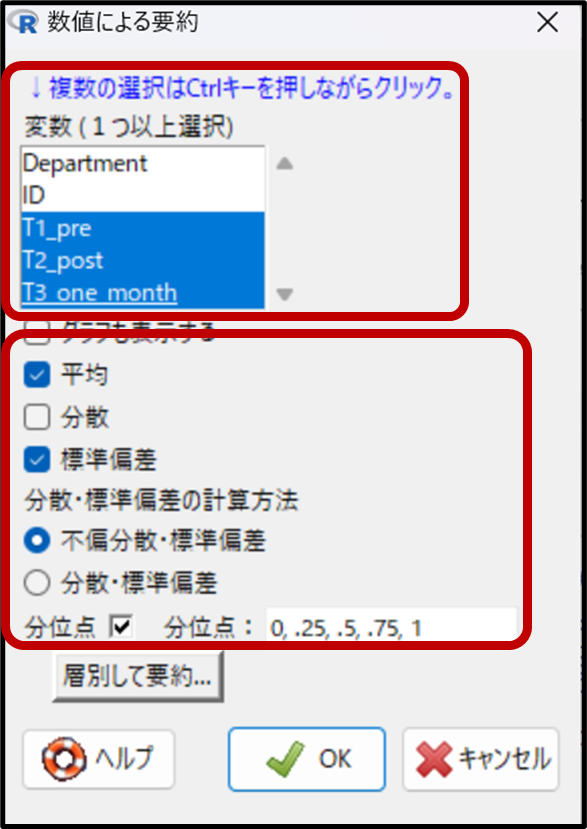
下記が、データを要約した出力結果です。
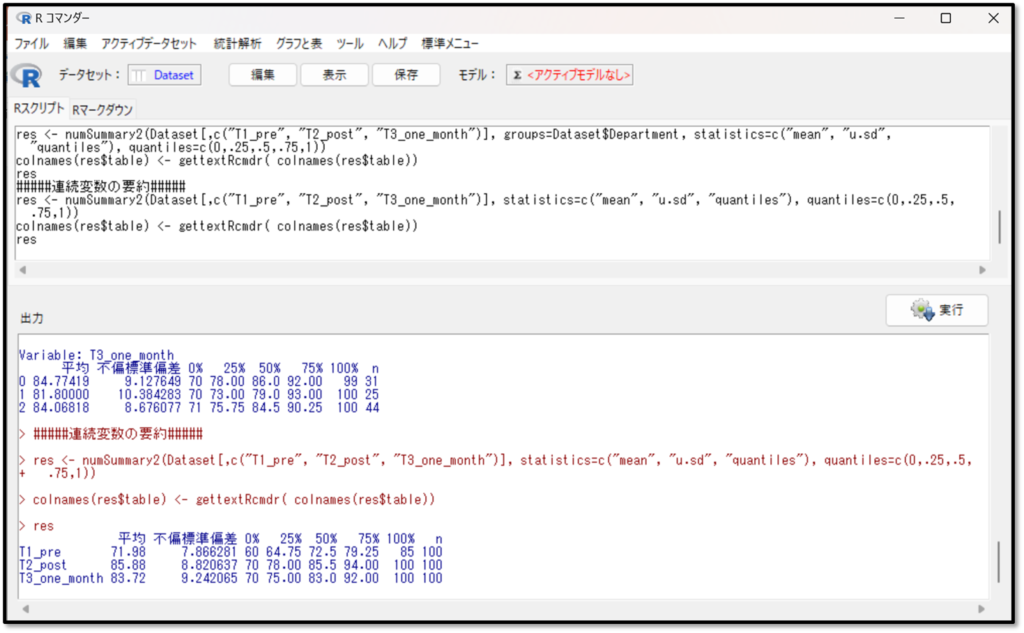
先ほども記載しましたが、一般的な要約したデータの結果の見方の復習です。正規分布に従うパラメトリック検定の場合は、代表値は「平均」を、データのばらつきは「標準偏差」を確認します。また正規分布に従わないノンパラメトリック検定の場合は、代表値は「中央値(50%) 」、データのばらつきは「四分位範囲」を確認します。
今回は正規分布に従わないデータを扱うノンパラメトリック検定なので、代表値は「中央値(50%)」、データのばらつきは「四分位範囲」を確認します。
今回の結果を見てみましょう。

T1_pre(プレテスト)のデータの要約を見ると、中央値(50%)が72.5点、四分位範囲(25%~75%)が64.75点~79.25点であることが分かります。
まとめ

分散分析と多重比較法は、看護研究において重要なツールです。これらを適切に理解し使用することで、より信頼性の高い研究結果を導くことができます。本記事が、これらの統計手法を学ぶ一助となれば幸いです。

この記事があなたの研究のお役に立てることを願っています。
今回は“対応のある”データを用いた分散分析・多重比較法を実際に行う方法を解説しました。分散分析・多重比較法の概要を知りたい方は下記を参照してください。












コメント