Last Updated on 2024年4月22日 by カメさん
こんにちは！看護師のカメさん(@49_kame)です。
この記事は10分程度で読めます。
今回は統計解析ソフトEZRを使用して実際に分散分析・多重比較（対応のないデータ）を行う方法を解説します。
分散分析（ANOVA）と多重比較法は、統計学における２つの基本的な手法であり、科学研究やビジネス分析など、多岐にわたる分野でのデータ解析に不可欠な役割を果たします。これらの手法を適切に理解し使用することで、データの背後にある真実を明らかにし、より信頼性の高い結論を導くことが可能となります。しかし、これらの統計手法の複雑さは、初学者にとって難易度が高いことも事実です。そこで本記事では、分散分析と多重比較法の基本原理から実際の適用方法に至るまで、初学者でも理解しやすい形で詳細に解説します。
本記事では、これらの手法の概念を明確にするために、実際のデータセットを用いた例を紹介します。また、統計ソフトウェアを使用した分析プロセスの基本ステップも解説し、読者が自身のデータにこれらの手法を適用することができるように解説していきます。
データ解析の世界は、複雑でありながらも、深い洞察と価値ある発見に満ちています。この記事が分散分析と多重比較法の基本を理解する一助となれば嬉しいです！
このブログでは統計解析ソフトしてEZRを使用しています。EZRは無料かつ精度も高い統計解析ソフトであるためおすすめです。EZRの概要とインストール方法については【EZRの概要とインストール方法】看護研究を変える！EZRで効率的な統計解析を参照してください。
はじめに
まずは分散分析・多重比較を行うための基礎知識を解説します
分散分析とは？
分散分析(ANOVA)は、３つ以上のデータ間で平均値に差があるかどうかを検証する統計手法です。平均値の比較において、複数のサンプル群間での差を一度に検討できるため、効率的な方法とされています。ただし分散分析では、「どこかのグループ間に差があるだろう」ということだけが分かります。さらに詳細な分析は多重比較法を実施します。
多重比較法とは？
多重比較法は、群間の差を個別に検討する手法です。分散分析で群間に差があると判断された場合、どの群が他と異なるのかを特定するために使用されます。つまり分散分析の結果、グループの間のどこかに差があることが分かったら、どのグループ間に差があるかを、多重比較法で判定します。
分散分析や多重比較法の概要を知りたい方は【分散分析：概要編➀】看護研究の疑問を解決「3つ以上の”対応のない”データを分析しよう」・【分散分析：概要編②】看護研究の疑問を解決「3つ以上の”対応のある”データを分析しよう」を参照してください。
対応のないデータと対応のあるデータとは？
対応のないデータとは、互いに独立したグループ間で比較が行われる場合です。また対応のあるデータは、同じ被験者が異なる条件下（同一人物の前後テストなど）で測定されたデータなどを指します。
対応のないデータの分散分析とは？
対応のないデータを用いた分散分析とは、３つ以上のグループからそれぞれ収集するデータを比較する分析のことです
例えば、3群に対してケアを行い効果を比較する分析などです
対応のあるデータの分散分析とは？
対応があるデータを用いた分散分析とは、１つのグループから収集する３つ以上のデータを比較する分析のことです
例えば、１グループへの介入前後、1カ月後の点数の比較などです
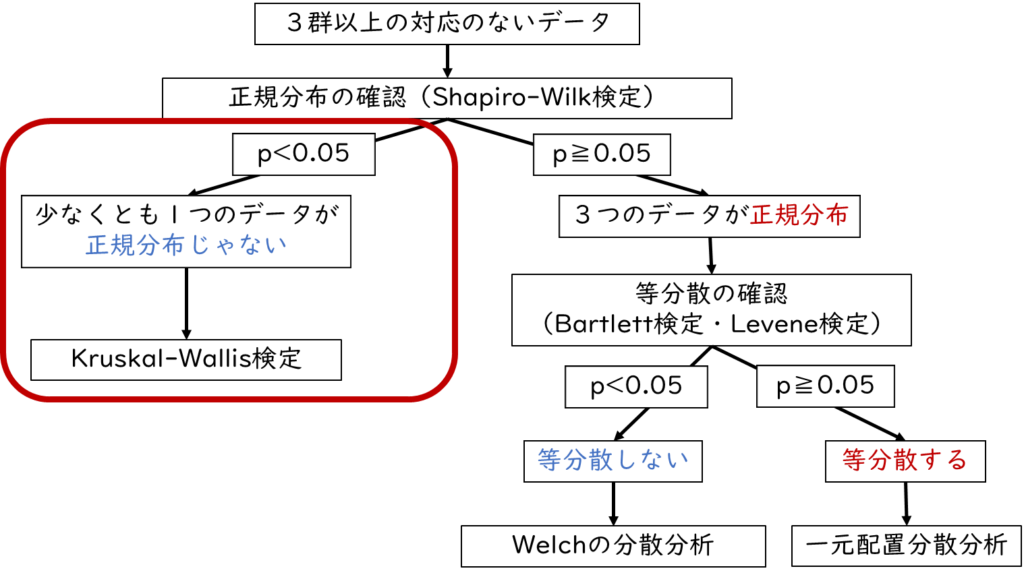
分散分析・多重比較法の基本的な流れ
下記が基本的な分散分析・多重比較法の流れになります。
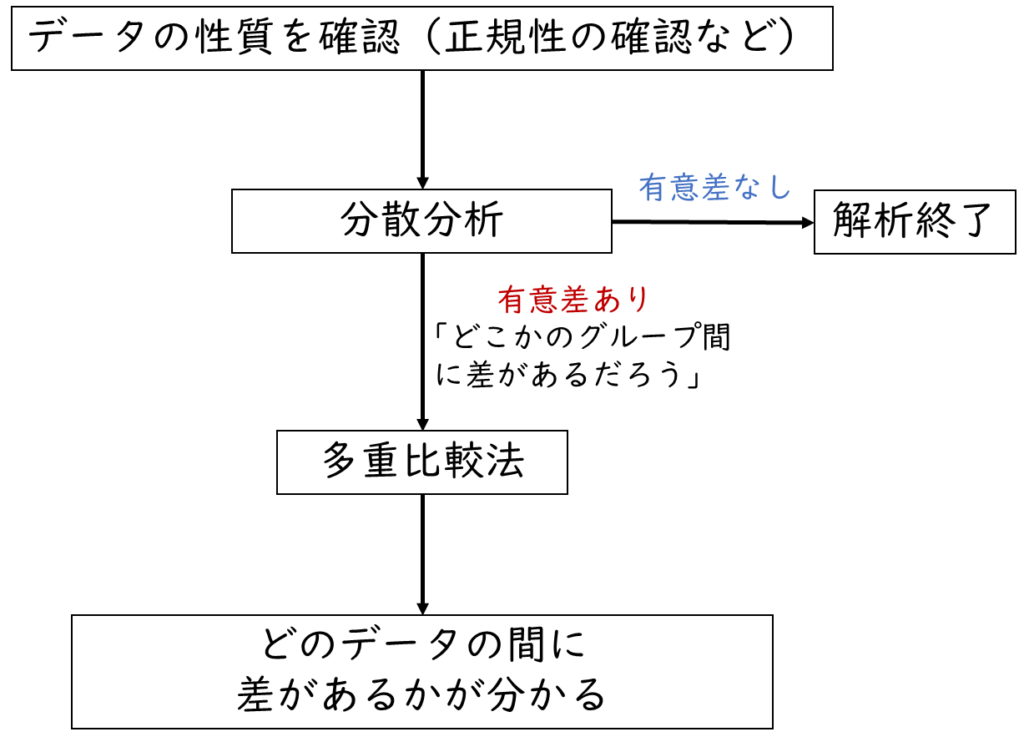
まずはデータの性質（正規分布かどうかなど）を確認し、その上で分散分析を行います。分散分析が有意でなければその時点で解析終了となります。
もし分散分析の結果が有意であれば、どこかのグループ間に差があることが分かります。そのため、どこのグループ間に差があるかを調べるために多重比較法を行います。多重比較法を行うことで、どのグループとどのグループの間に差があるかが分かります。
分散分析で、差があるかどうかを簡単に確認して、どこかに差があるのであれば、多重比較法で詳細に分析するイメージだね。
分散分析・多重比較法には種類がある
分散分析・多重比較法には、他の統計解析方法と同様に種類があります。解析方法の種類の選択にはデータの種類（対応あるデータ or 対応のないデータ）、正規性、等分散性などの前提条件を確認する必要があります。これらの条件に応じて適切な手法を選択します。
分散分析・多重比較法は以下の4つのポイントで決まります。
- ➀「対応のあるデータ」か 「対応のないデータ」
- ②「正規分布」 か「正規分布でない」
- ③「等分散する」か 「等分散しない」
- ④「球面性を仮定できる」 か「球面性を仮定できない」
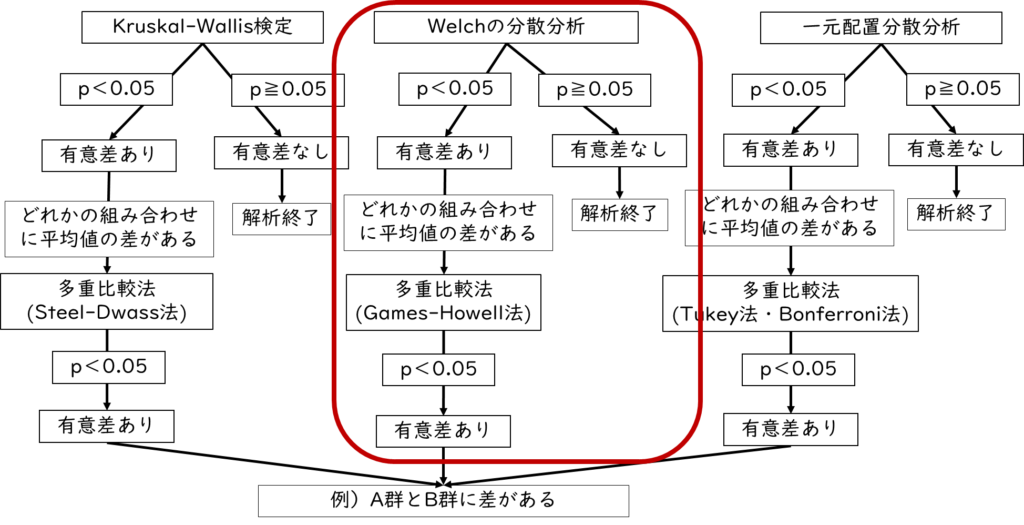
上記のポイントを踏まえた分析方法の早見表が下記になります。セルの中の赤い矢印が多重比較法です
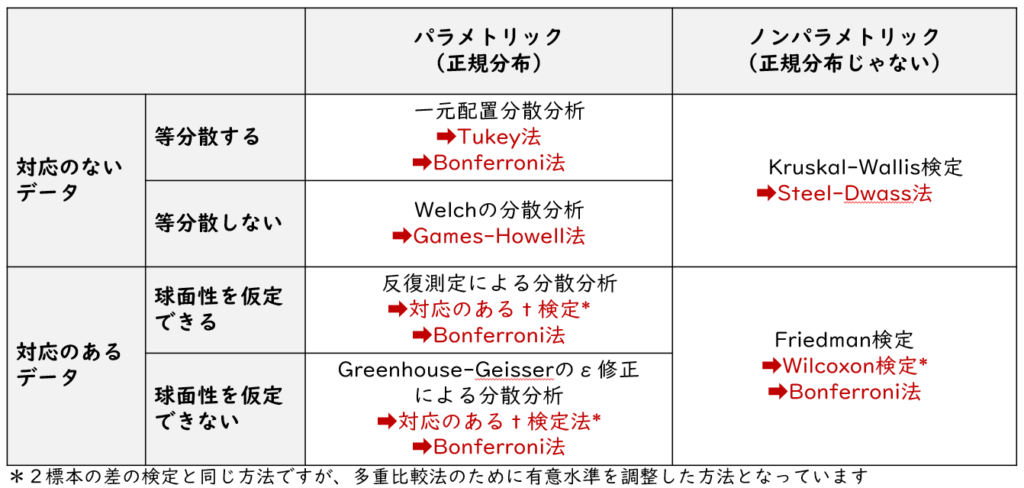
収集したデータの特徴に合わせて分析方法を検討しよう。今回は対応のないデータに焦点を当てて解説するよ。
EZRで行う分散分析・多重比較法の検定手順（“対応のない”データ）
今回はEZRを使用して「対応のないデータ」の分散分析・多重比較法について解説します。
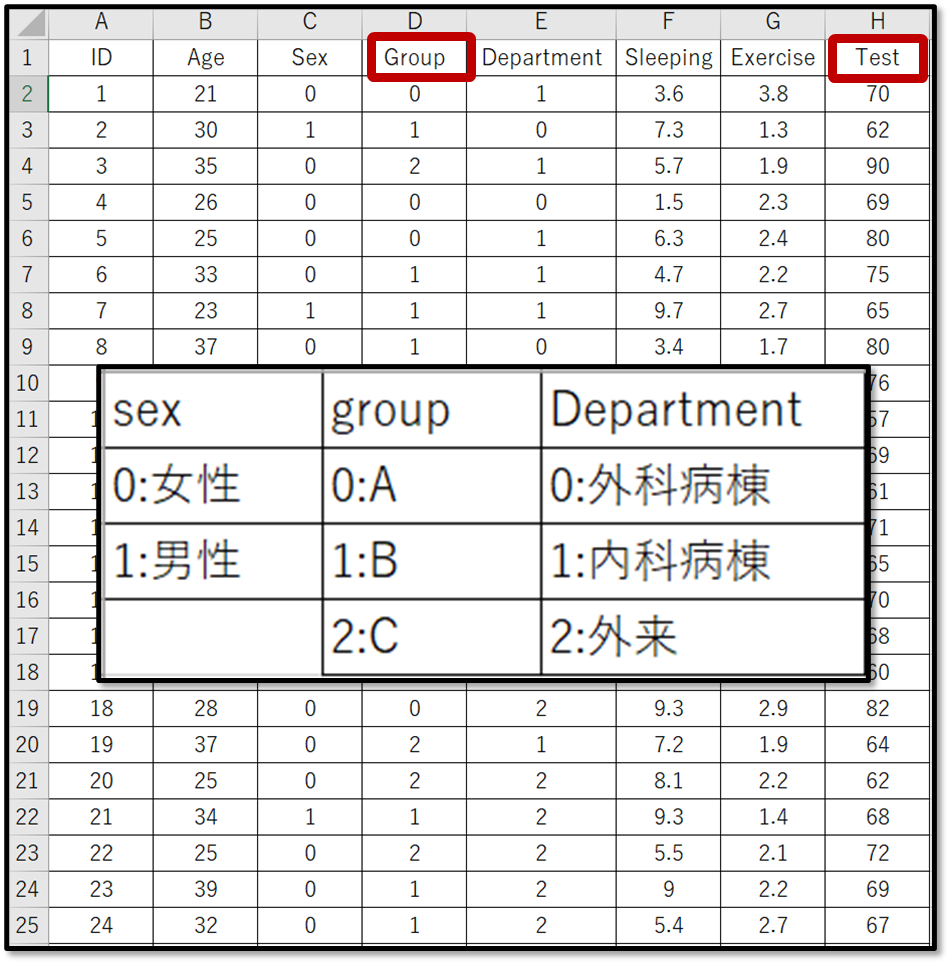
今回使用するデモデータ
今回は下記のデモデータ（一部抜粋）を使用します。
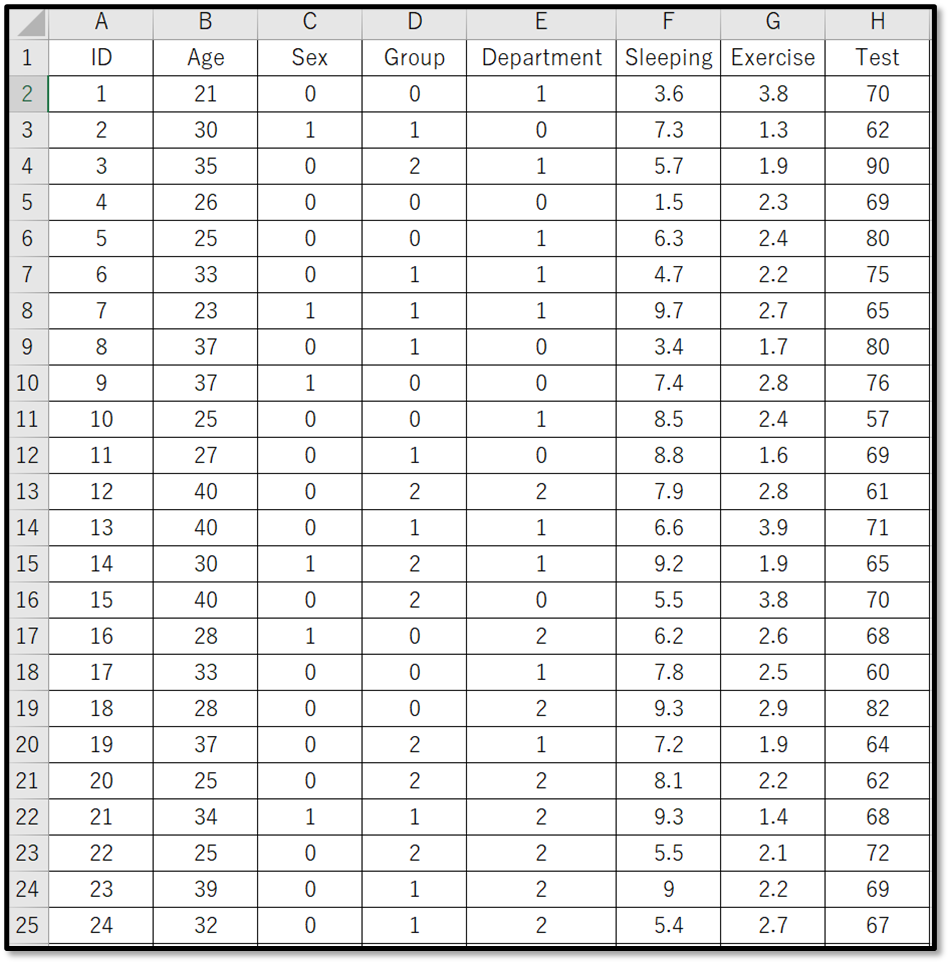
表示しているのは、デモデータの一部です。デモデータは下記からダウンロードできるので使ってみてください。
ランダム関数で作成しているため、今回の結果とズレが出るかもしれませんが、ご了承ください。
こちらのデモデータを読み込んだ後の段階から解説します。データの読み込み方法については、【統計解析ソフトにデータを入力】看護研究初めの一歩：EZRにデータセットを入力しよう！を参照してください。
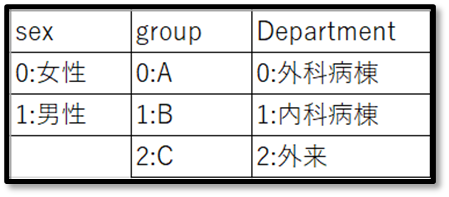
今回は対応のないデータとして、グループA、グループB、グループCの３つのグループのテストの点数を比較します。今回のデモデータはすでにコード化しています。グループのコード化は、0がAグループ、１がBグループ、2がCグループです。
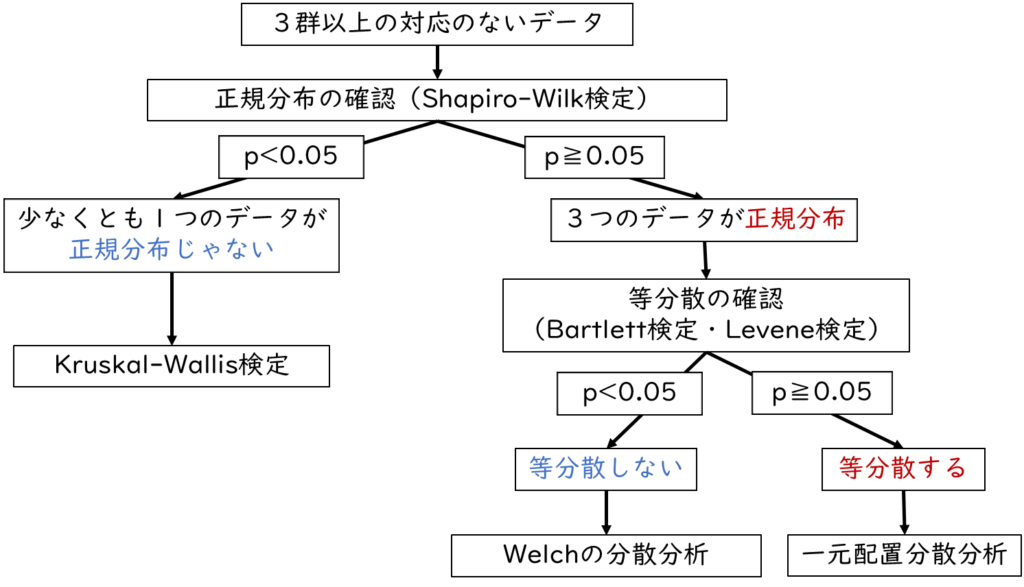
「対応のないデータ」の分散分析・多重比較法の検定手順
下記が対応のないデータについての分散分析・多重比較法の手順です。下記の手順に従って解説していきたいと思います。
まずはグループA（０）、グループB（1）、グループC（2）の３つのグループのテストの点数についてそれぞれ正規分布を確認します。今回は正規分布の確認手順は割愛します。詳しく知りたい方は【正規分布とは？：実践編】看護研究の疑問を解決「EZRで正規分布を確認しよう」を参照してください。
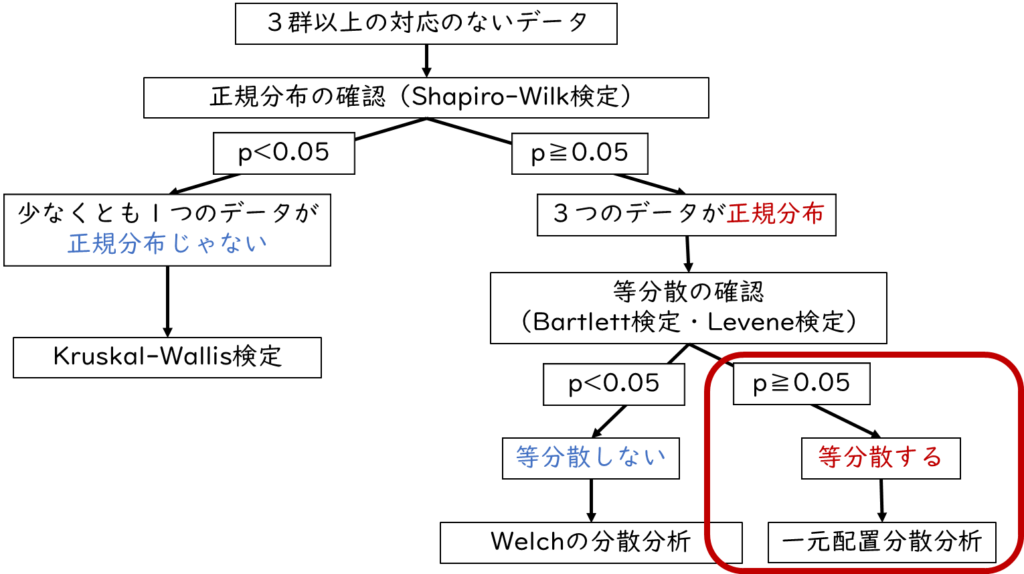
３つのデータが正規分布している場合
３つのデータがどれも正規分布している場合、次は等分散の確認を行います。
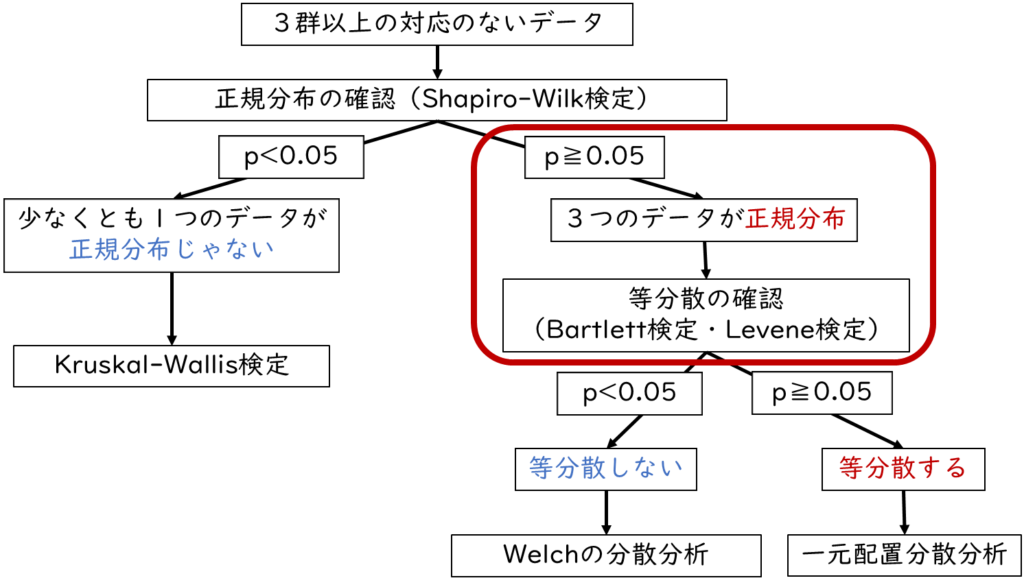
デモデータの中の「データ１」と記載されたデータが３つのデータがどれも正規分布になるように調整したデータだよ。
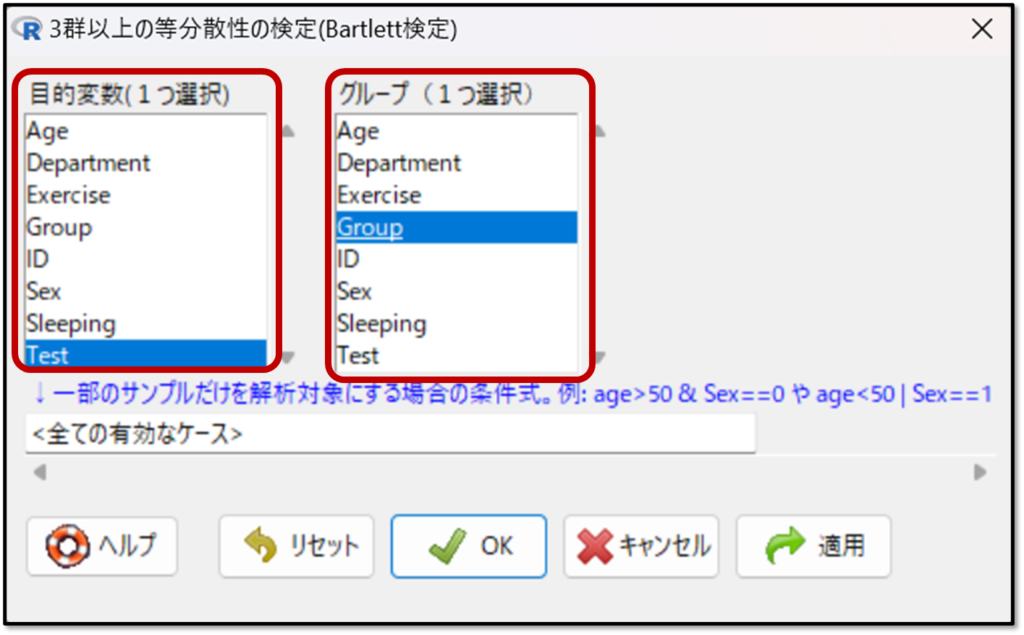
EZRの画面で「統計解析」→「連続変数の解析」→「3群以上の等分散性の検定（Bartlett検定：バートレット検定）」を選択します。
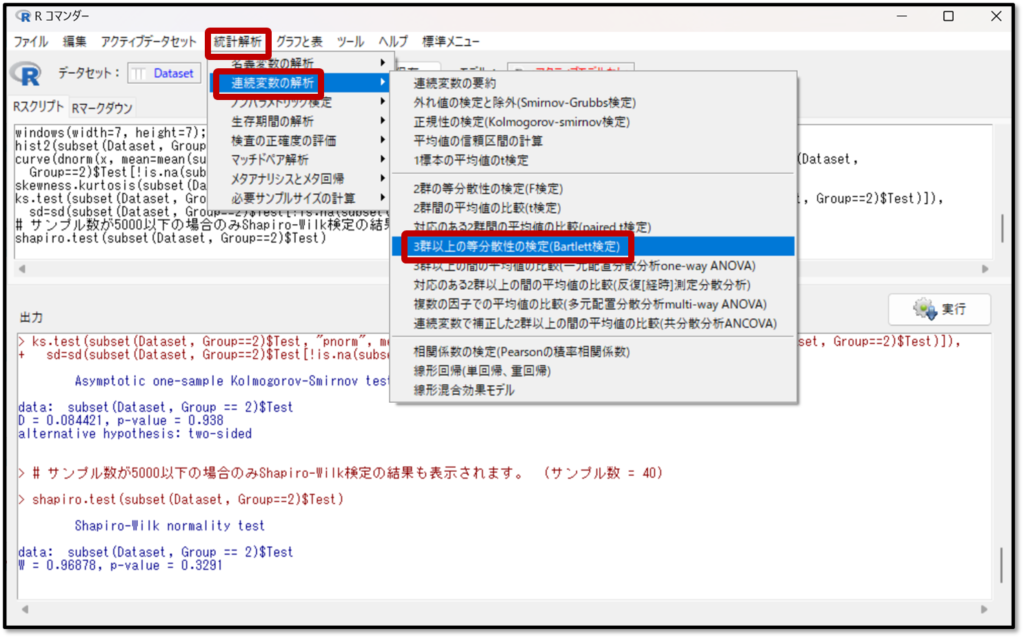
次に下記の画面になるので「3群以上の等分散性の検定」をしたい変数として「Test」を選択し、分類として「Group」を選択します。
下記がA・B・Cグループのテストの点数の等分散性の検定の結果です。
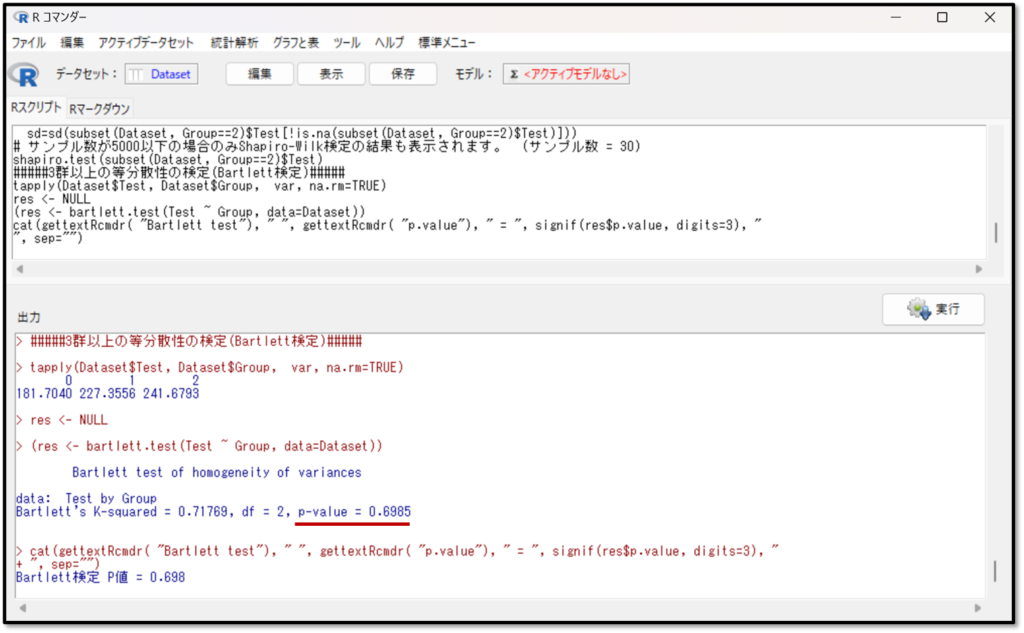
出力結果を見るとpバリューは0.6985、p値が0.05以上なので等分散していると判断します。上記のように3群以上の”対応のないデータ”で正規分布かつ等分散している場合は「一元配置分散分析」となります。
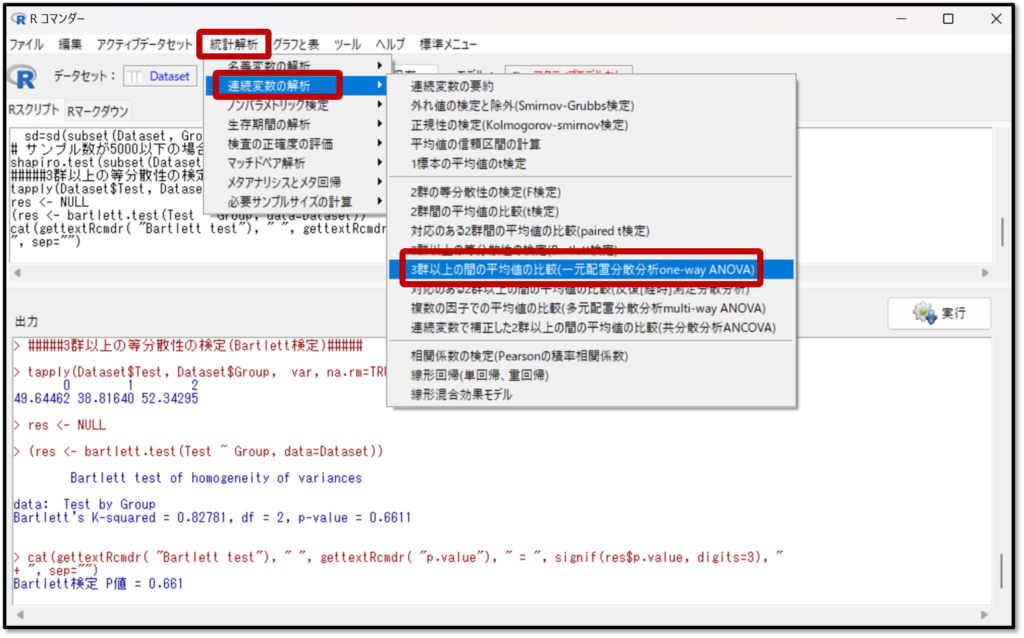
「一元配置分散分析」を実施する方法をみていきましょう。EZRの画面で「統計解析」→「連続変数の解析」→「3群以上の間の平均値の比較（一元配置分散分析 one-way ANOVA）」を選択します。
分散分析は英語でanalysis of varianceと呼ばれ、略してANOVA （アノーバ）と呼ばれたりします。今回は、テストの点数という1つの因子だけ見てるのでワンウェイ アノーバです。因子が2つになるとツーウェイ アノーバと呼ばれます。
下記が一元配置分散分析の操作画面ですが、事前に赤枠部分の多重比較法についても検討します。
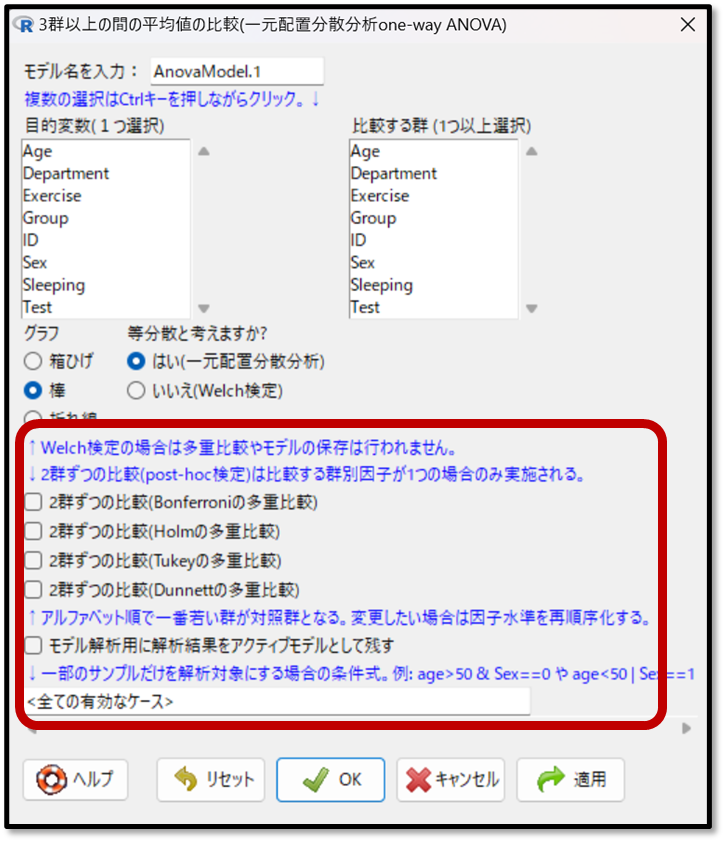
本来であれば分散分析を行い有意差がある場合に、次に多重比較法の解析に移行します。しかしEZRでは事前に多重比較法も選択し、分散分析と多重比較法の結果が同時に算出されます。
今回は一元配置分散分析にて分散分析を行うので、多重比較法はTukey法（テューキー法）もしくはBonferroni法（ボンフェローニ法）を選択します。
それでは下記の操作画面に戻ります。分散分析をしたい変数と実施する多重比較法を選択します。目的変数がTestの点数で、比較する群としてGroupを選択します。また等分散性の検定の結果、等分散であることが分かっているので、「等分散と考えますか？」の質問項目の「はい」にチェックを入れます。
最後に多重比較法を選択します。EZRにはTukey法（テューキー法）もしくはBonferroni法（ボンフェローニ法）もあるので、どちらも選択しましょう。
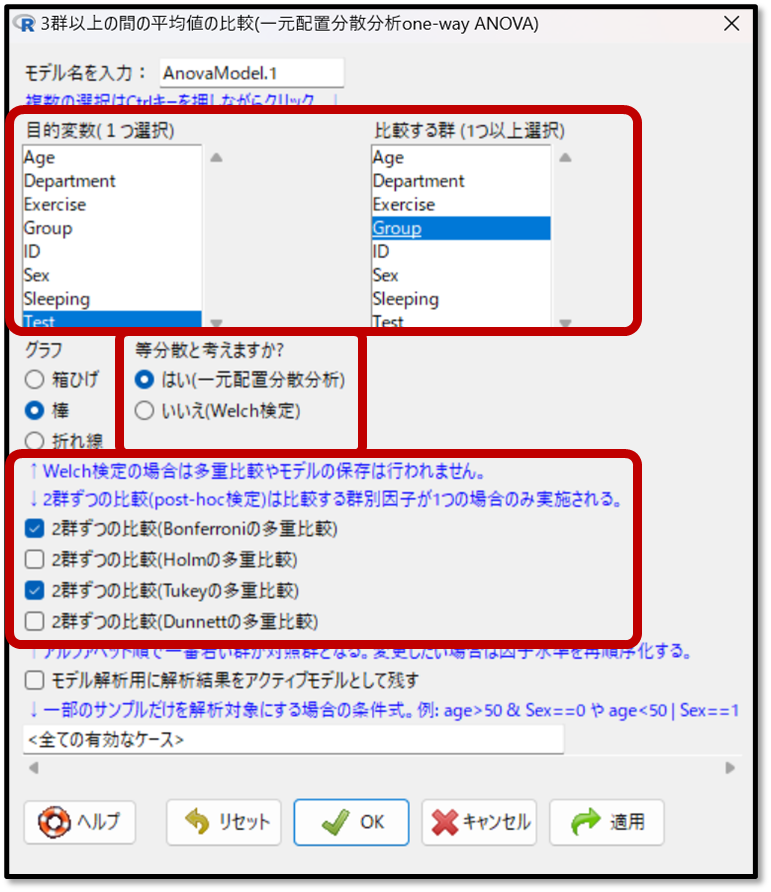
Bonferroni法（ボンフェローニ法）はオーソドックスな方法ですが有意差がでにくい特徴があるので、比較的厳密に検定したい場合にオススメです。またTukey法（テューキー法）は有意差が出やすいとされています。どちらの結果を採用するかは、研究の厳密性で決めましょう！
下記が一元配置分散分析の出力結果です。数値による出力結果と、図による出力結果が表示されます。
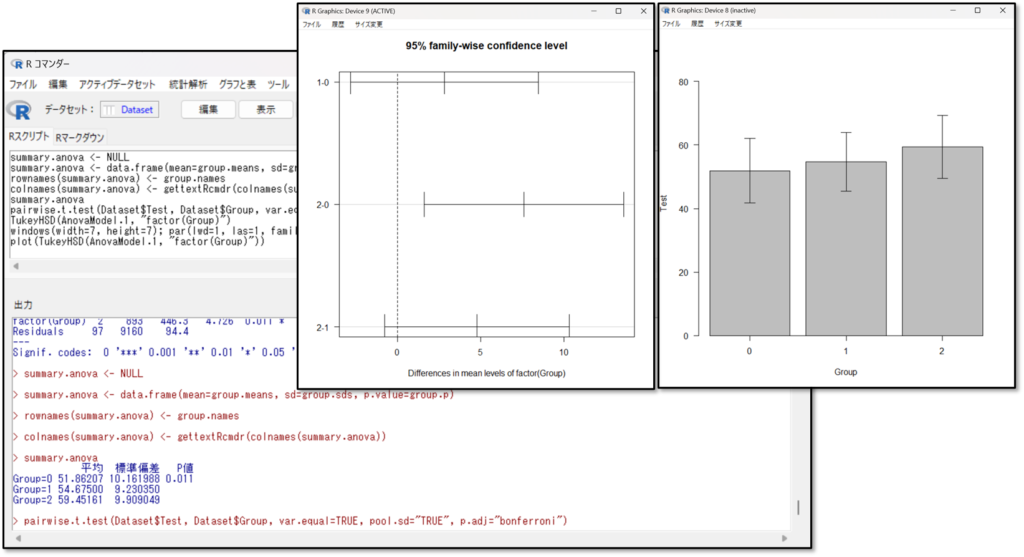
結果の見方を解説します。まずは図の結果から解説します。一元配置分散分析の出力結果では、2つの図が出力されます。左の図の「95% family-wise confidence level」とは各群の平均値の差の95％信頼区間です。そして右の図が各データの「棒グラフ」です。
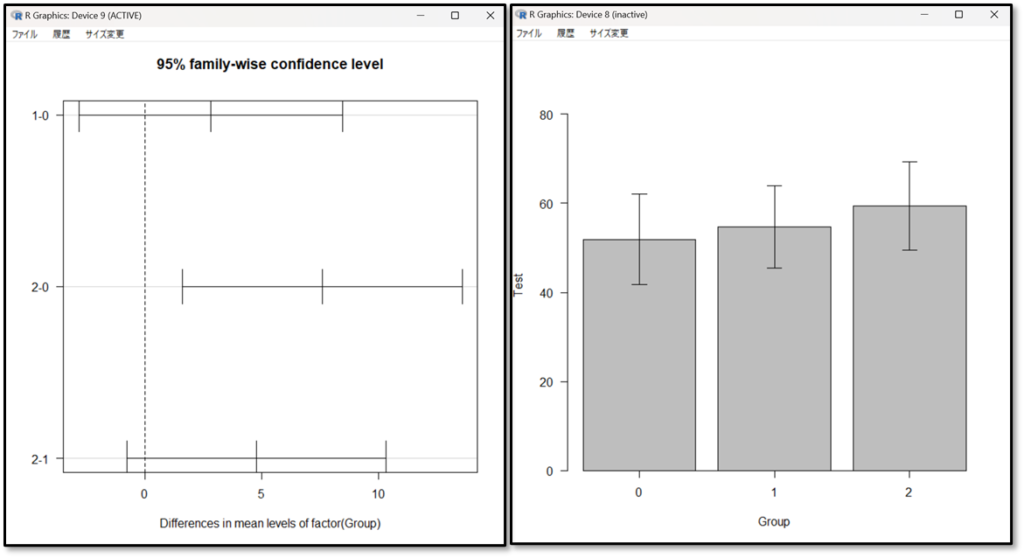
まずはデータ間の差を視覚的に確認しましょう
次に数値の出力結果の見方です。数値の出力結果は各群のデータの要約である「平均」「標準偏差」「ｐ値」を確認しましょう。今回はp値が0.05未満であれば統計的に有意差があると事前に設定したと仮定して話を進めます。p値が0.05未満であれば、3群のどこかに有意な差があると判断し、多重比較法の結果を確認します。
p値が0.05以上であれば、3群のどこにも有意な差はないので解析終了となるよ
今回の結果を見てみましょう。
今回はp値が０.011 なので3群のどこかに有意な差があると判断します。続いて多重比較法の結果を確認しましょう。
まずは多重比較法として、Bonferroni法（ボンフェローニ法）の結果の見方を説明します。Bonferroni法（ボンフェローニ法）は表の形で算出されます。それぞれのデータの組み合わせに対応するp値が出力されており、p値が0.0５未満であれば、その組み合わせで有意な差があると判断します。下記がBonferroni法（ボンフェローニ法）の出力結果です。
出力結果上分かりにくいですが下記の図のように行の0,1をAグループ,Bグループ、列の1,2をBグループ,Cグループと当てはめて考えます。
例えば左下の、0（Aグループ）と2（Cグループ）のテストの点数の比較では、p値が0.0096と出力されています。つまりこの組み合わせに有意な差があったことがわかります。
下記がコード化の説明だよ。
次にTukey法（テューキー法）の結果の見方を解説します。Tukey法（テューキー法）はBonferroni法（ボンフェローニ法）より見やすくなっています。各データの組合せ毎の「p値」が算出されているので確認します。p値がp<0.05であれば、そのデータの組み合わせに有意な差があると判断します。
下記がTukey法（テューキー法）の出力結果です。
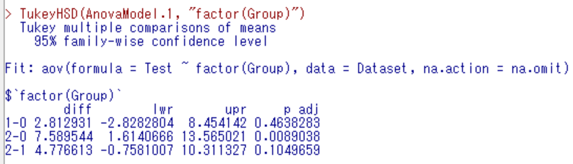
1-0とは１（Bグループ）と0（Aグループ）の組み合わせ、2-0とは2（Cグループ）と 0（Aグループ）の組み合わせ、2-1とは2（Cグループ）と1（Bグループ）の組み合わせのことを示しています
それでは2-0の組み合わせ、つまりCグループとAグループのテストの点数の組み合わせを見てみましょう。上記結果の「p adj」が「p値」です。「p 値」が0.0089038、つまりp値が0.05未満なので有意差ありと判断します。
これらの結果から、分散分析で3つのデータのどこかの組み合わせに差があることが分かって、多重比較法でＡグループとＣグループの組み合わせに差があったことが分かったね。
等分散していない場合は？
もし等分散の検定で、等分散していないことが分かったら、Welch（ウェルチ）の分散分析を使用します。
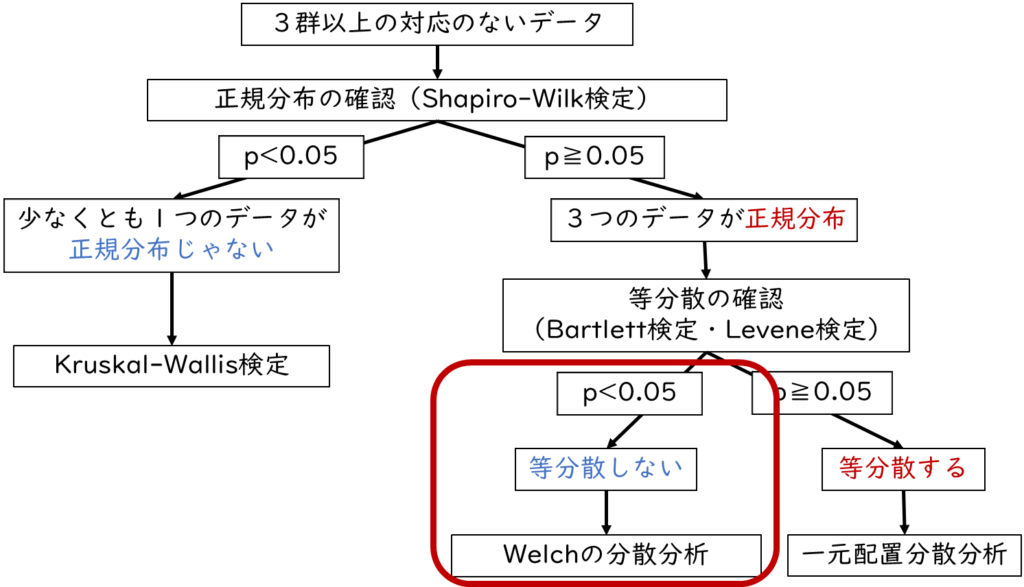
Welch（ウェルチ）の分散分析では、多重比較法としてGames-Howell（ゲームス・ハウエル）法を選択します
等分散していない場合は、下記の操作画面において「等分散と考えますか」の質問項目はいいえを選択します。また多重比較法では、Games-Howell（ゲームス・ハウエル）法を選択します。
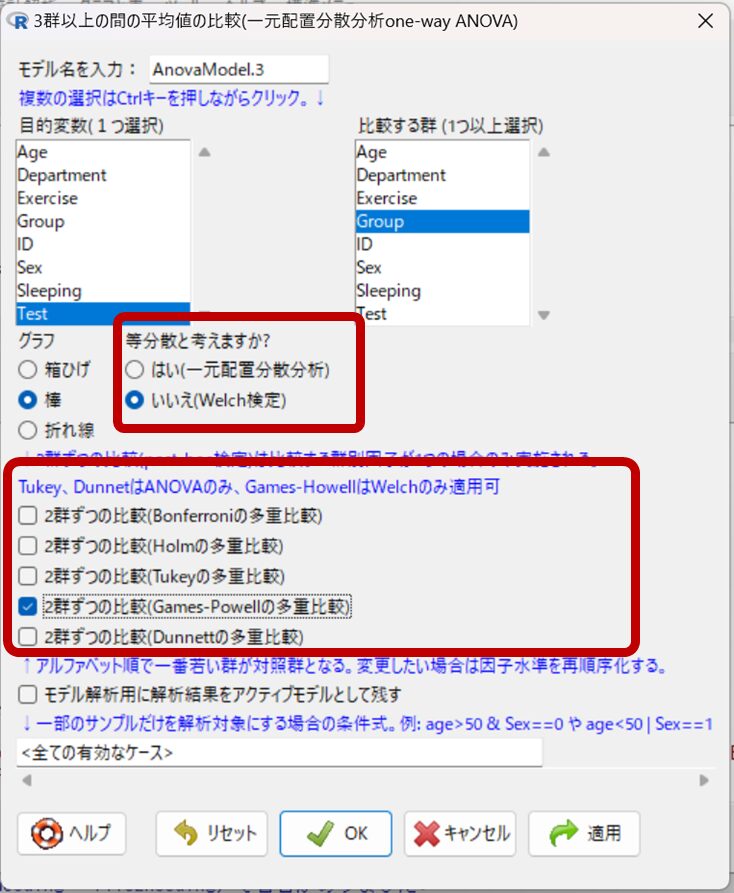
Games-Howell（ゲームス・ハウエル）法はVersion 1.62から追加されました。EZRを以前のバージョンで使っている人はアップデートしよう！
下記が等分散していない場合のWelch（ウェルチ）検定の結果です。
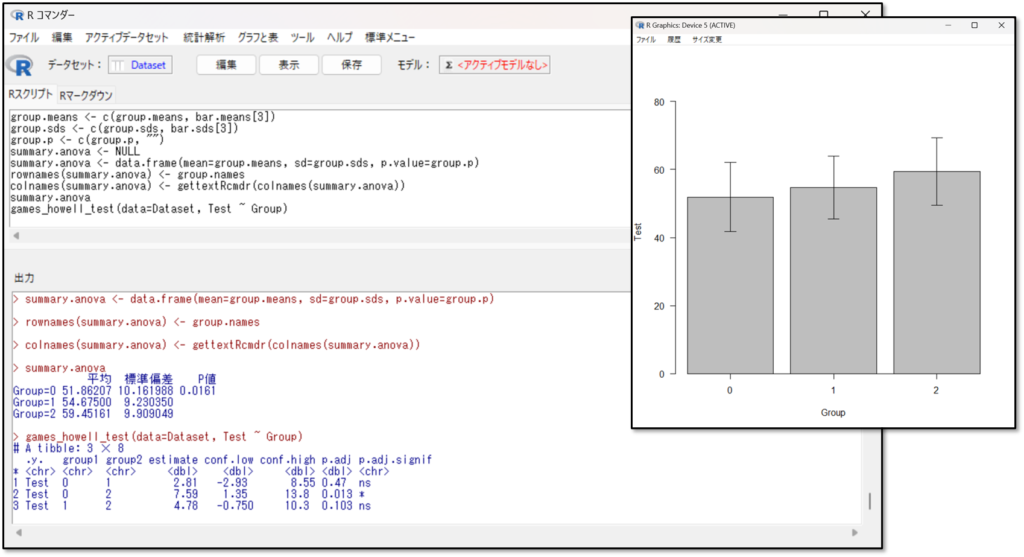
結果の見方は一元配置分散分析と同様です。まずは各群のデータの要約である「平均」「標準偏差」を確認します。続いて「ｐ値」を確認します。p<0.05であれば、3群のどこかに有意な差があると判断します。そのため、多重比較法の結果を確認します
今回の結果をみてみましょう。
p値が0.0161なので、3つの群間のどこかに有意な差があると判断します。続いて、多重比較法も見てみましょう。今回は等分散していないデータなので、Games-Howell（ゲームス・ハウエル）法を選択しました。
Games-Howell（ゲームス・ハウエル）法の結果の見方を解説します。各データの組合せ毎の「p 値」を確認します。p値がp<0.05であれば、その組み合わせに有意な差があると判断します。
今回の多重比較法の出力結果を見てみましょう。
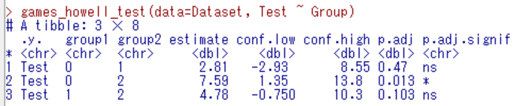
「0 1」とは0（Aグループ）と１（Bグループ）との組み合わせ、「0 ２」とは0（Aグループ）と2（Cグループ）と の組み合わせ、「1 2」とは1（Bグループ）と2（Cグループ）との組み合わせのことを示しています。
例えば今回だと、「0 2」つまりAグループとCグループの組み合わせのp値が0.013なので、この組み合わせに有意な差があったと判断します。
そもそも、等分散性自体が「確認は不要」という意見もあるよ。ですが等分散性を検定することが一般的なので、もし等分散していなかったら上記の手順で解析しよう！
３つのデータの少なくとも1つが正規分布していない場合
次にAグループとBグループ、Cグループの３つのデータのうち少なくとも1つのデータが正規分布していない場合の”対応のないデータ”の分散分析・多重比較法について解説します。
一部のデータが正規分布していなかった場合は、Kruskal-Wallis（クラスカルウォリス）検定を選択します。正規分布でないデータを扱うのでノンパラメトリック検定となります。
デモデータの中の「データ2」と記載されたデータが少なくとも１つのデータが正規分布にならないように調整したデータだよ。
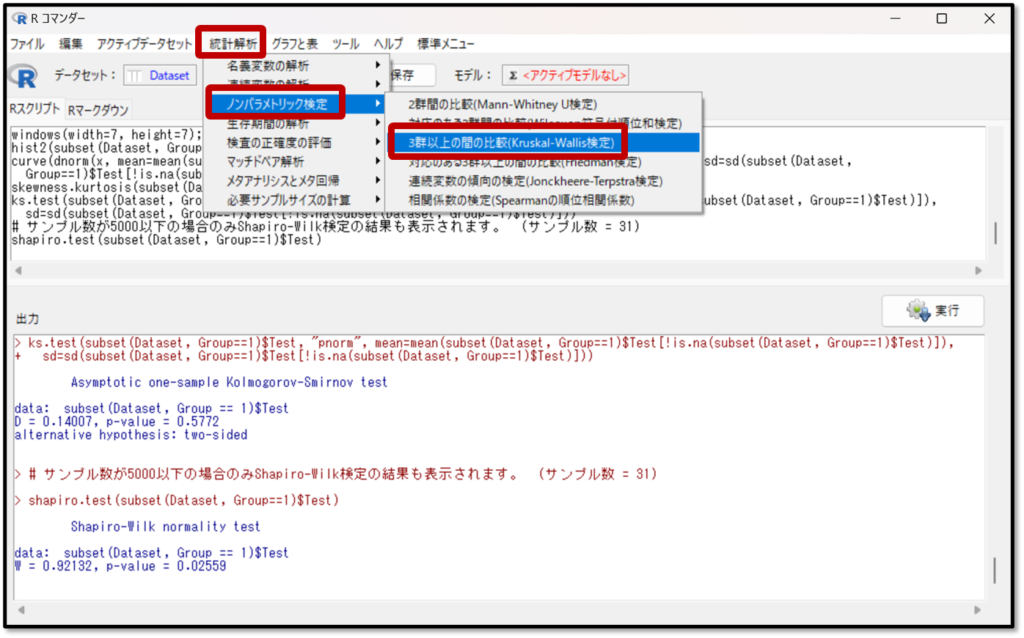
それでは解析を実施していきましょう。EZRの画面で「統計解析」→「ノンパラメトリック検定」→「3群以上の間の比較（Kruskal-Wallis検定）」を選択します。
下記の操作画面で、変数としてTestを選択します。そして比較する分類として、Groupを選択します。パラメトリック検定（正規分布のデータに対する検定）の時と同様に事前に多重比較法を選択します。
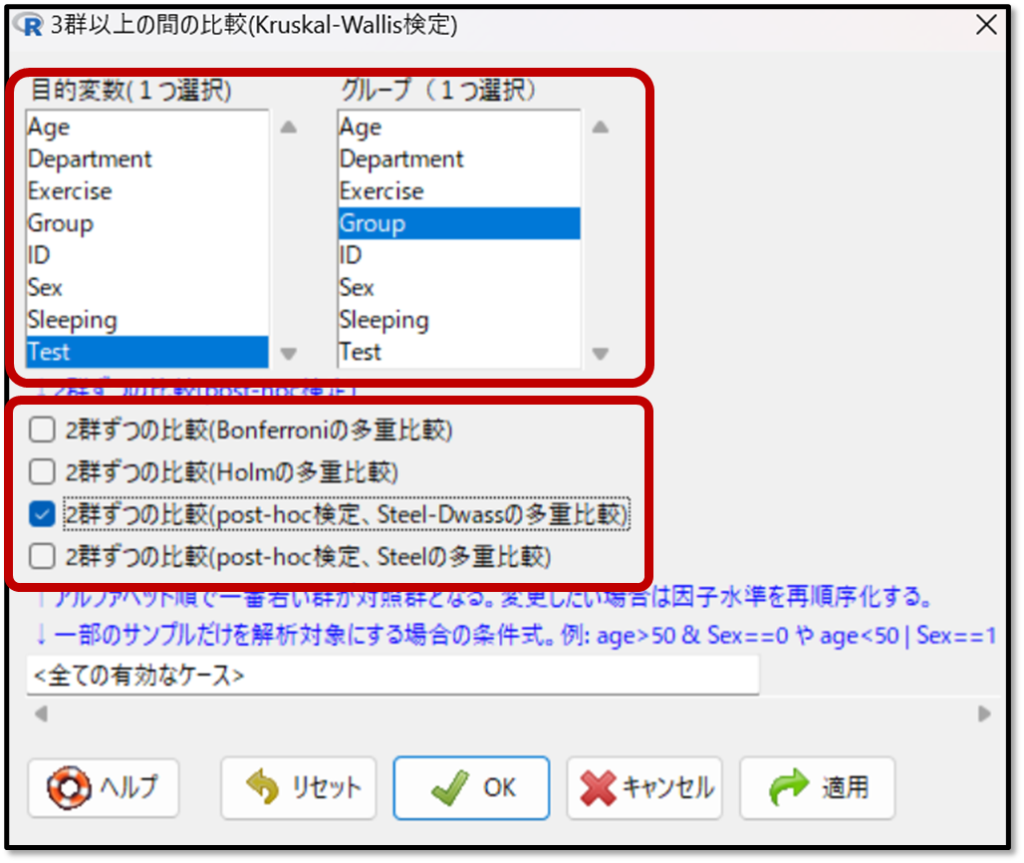
今回はKruskal-Wallis（クラスカルウォリス）検定なので、多重比較法はSteel・Dwass（スティール・ドゥワス）法となります。
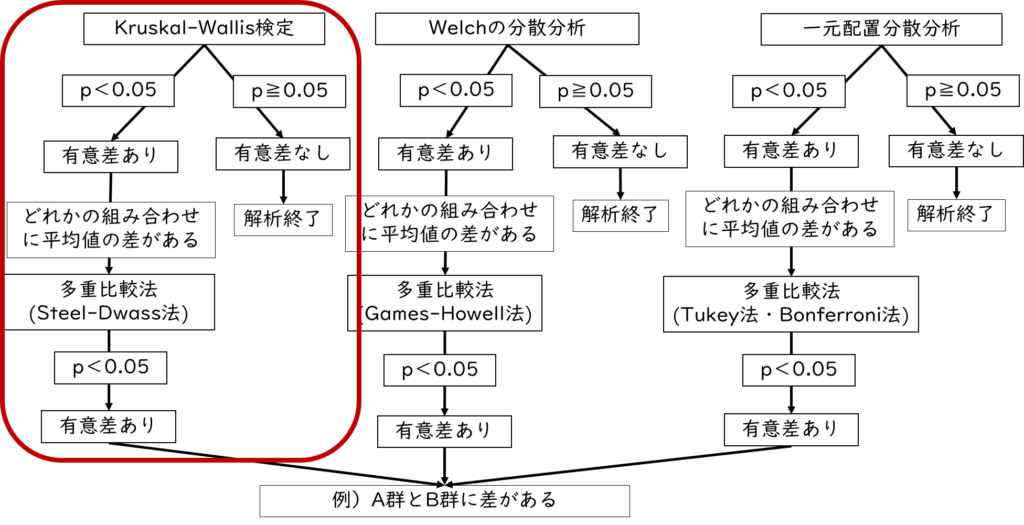
そのため先ほどの操作画面でSteel・Dwass（スティール・ドゥワス）法を選択しましょう。下記がKruskal-Wallis（クラスカルウォリス）検定の結果です。
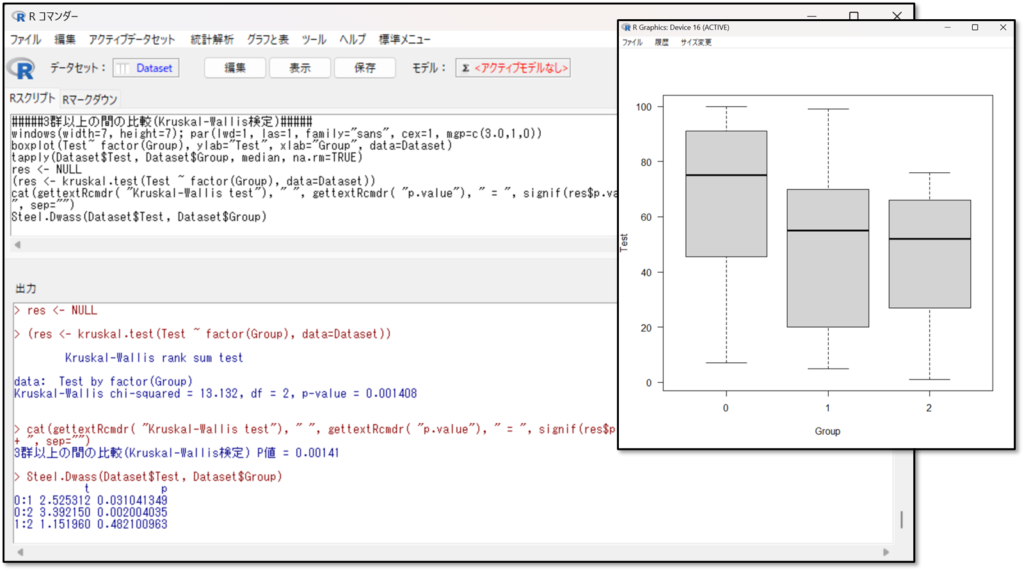
図と数値で出力結果が表示されます。結果の見方を解説します。まずは図の結果として、箱ひげ図が出力されるので、群間の差を視覚的に確認しましょう。
ノンパラメトリック法では図を箱ひげ図で表す
箱ひげ図とは四分位数（大きい順に並べて、パーセント表示したもの）を用いてデータの散らばりを表した下記のような図のことです。
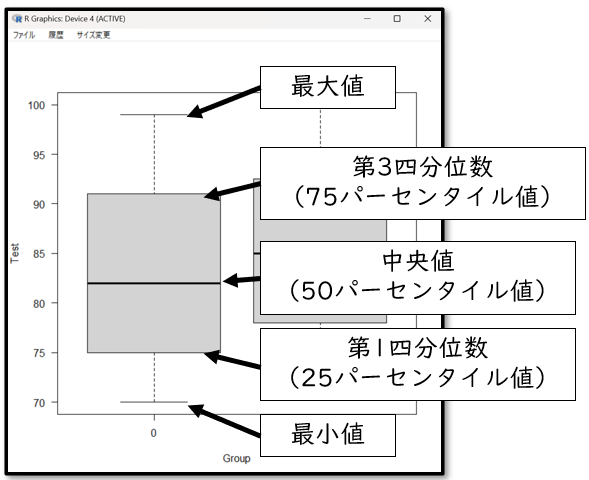
一番上の線、ひげの一番上は最大値です。ここは90パーセンタイル値を用いる場合もあります。次に長方形の一番上の返が第3四分位数（75パーセンタイル値）つまり、大きい順に並べて75％の値、長方形の真ん中が、中央値（50パーセンタイル値）、大きい順に並べて真ん中の値です。そして長方形の下の返が第1四分位数（25パーセンタイル値）、大きい順に並べて25％の値、そして最後に一番下の線、ひげの一番下が最小値です。ここは10パーセンタイル値を使用することもあります。
パーセンタイル値は、パーセント表示した際に使用する用語だよ。
次に数値の出力結果について解説します。今回はパラメトリックの時と異なり、平均や標準偏差などのデータの要約が算出されません。そのため、確認するのはp値のみです。「ｐ値」を確認し、p<0.05であれば、3群のどこかに有意な差があると判断し、多重比較法の結果を確認します。
p≧0.05であれば、3群のどこにも有意な差はないので解析終了となるよ
今回の分散分析の結果を見てみましょう。まずは箱ひげ図です。
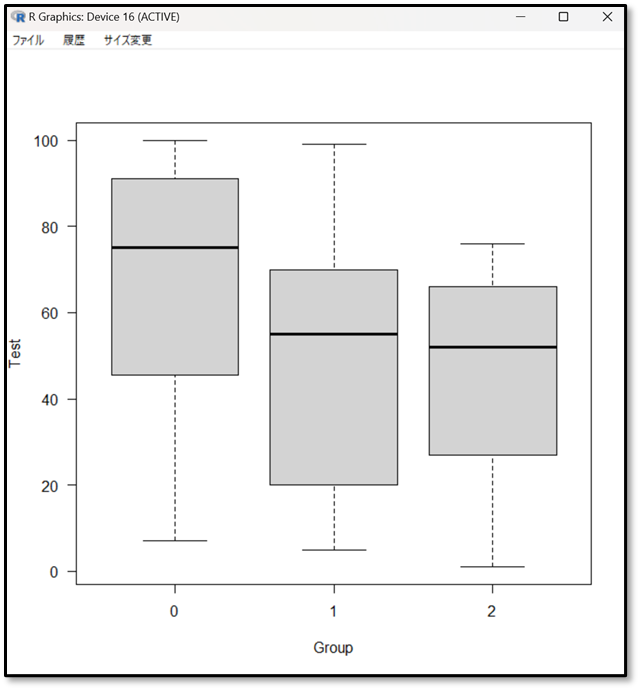
箱ひげ図を見ると視覚的に差がありそうなことが分かります。次にp値の結果を見てみましょう。
p値が0.00141なので有意差ありと判断します。次に多重比較法の結果も見てみましょう。下記がSteel・Dwass（スティール・ドゥワス）法の結果です。
Steel・Dwass（スティール・ドゥワス）法では各データの組合せ毎の「p値」を確認します。0：１とはAグループとBグループの組み合わせ、0：２とはAグループとCグループの組み合わせ、1：2とはBグループとCグループの組み合わせのことです。p値がp<0.05であれば、その組み合わせに有意な差があると判断します。
下記がコード化の詳細だよ。
上記の出力結果を見ると、０：１（AグループとBグループの組み合わせ）のp値が0.03、0：2（AグループとCグループの組み合わせ）のp値が0.002となっています。つまり、この2つの組み合わせにおいて有意な差があったと判断します。
EZRにて「Kruskal-Wallis検定」を行う場合はデータの要約（中央値など）は出力されません。そのため、要約したデータを算出するための追加の操作が必要になるよ。ちなみに先ほどのパラメトリック法の時は、データの要約（平均値・標準偏差）が算出されていたね。
要約したデータ（中央値・四分位範囲）の算出方法
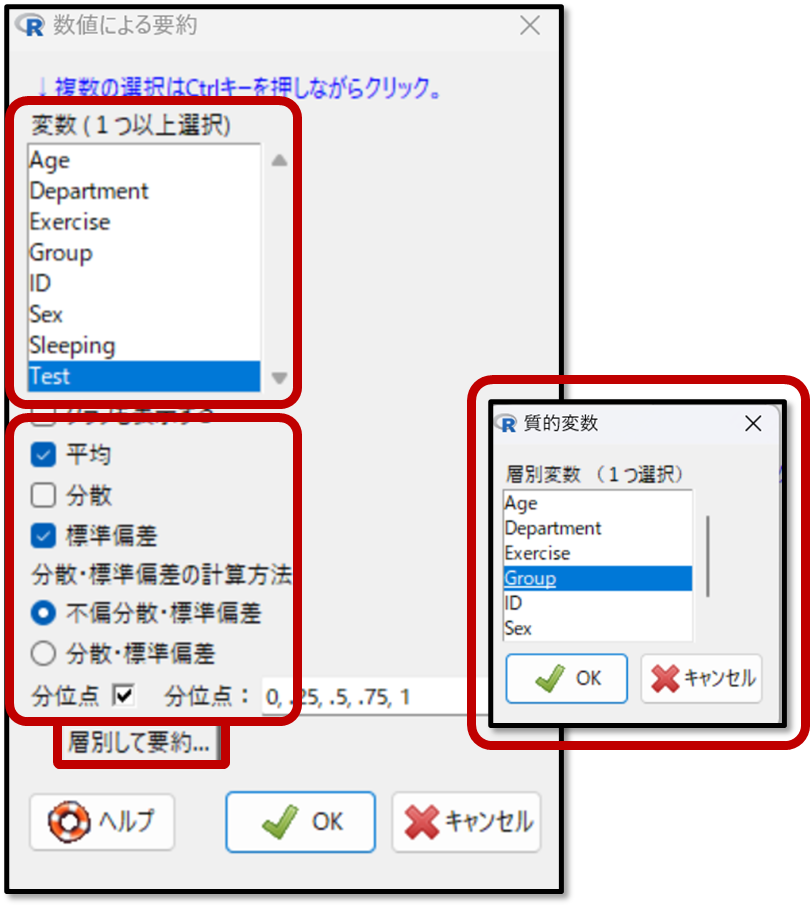
EZRでのデータの要約方法を解説します。EZRの画面から「統計解析」→「連続変数の解析」→「連続変数の要約」を選択します。
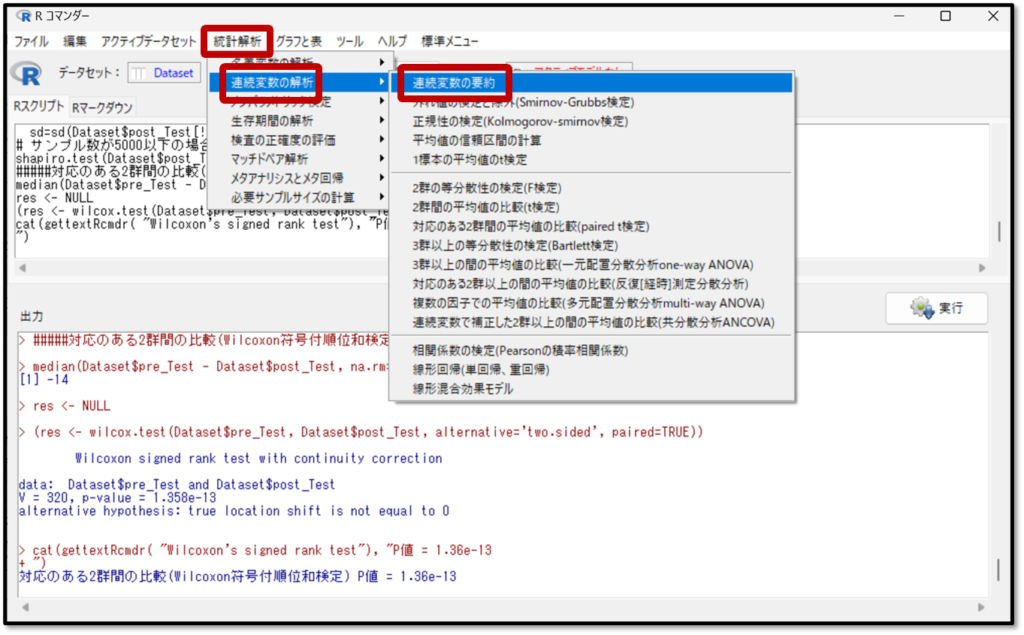
次に下記の画面にて要約したい変数としてTestを選択します。平均や標準偏差も算出することができますが、今回は正規分布していないデータなので、最低でも分位点に✓が入っていれば中央値と四分位範囲を確認することができるので問題ありません。
「層別して要約」を選択してGroupを選択すると、グループ毎のデータの要約を確認することができるよ！
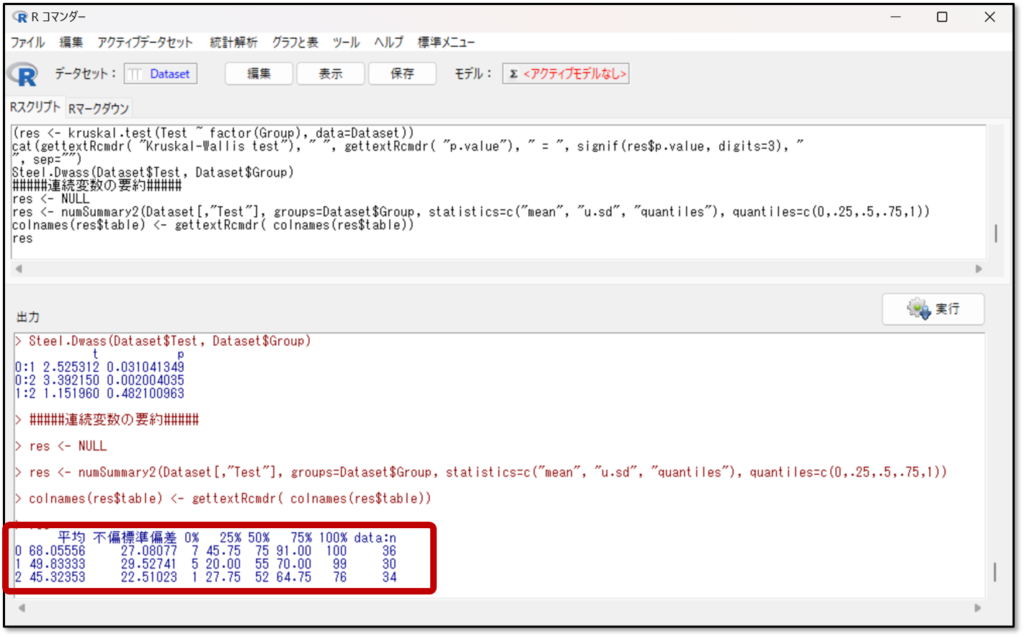
下記が、データを要約した出力結果です。
正規分布に従うデータの要約の場合は、代表値として「平均」を、データのばらつきとして「標準偏差」を確認します。また正規分布に従わないデータの要約の場合は、代表値は「中央値（50％） 」、データのばらつきは「四分位範囲」を確認します。今回は正規分布に従わないデータの要約を行っているので「中央値（50％）」と「四分位範囲」を確認します。下記の図がイメージです。
上記の今回の出力結果の、0（Aグループ）のデータを見てみましょう。中央値は50％と書いてあるところなので「75」、四分位範囲は25％の「45.755」から75％の「91」の範囲です。
ちなみに四分位範囲でなく、最大値・最小値の範囲で表現する方法もあるよ！
まとめ
分散分析（ANOVA）と多重比較法は、統計学においてデータの群間比較における重要な手法であり、複数のグループ間での平均値の比較においてその効果を発揮します。
今回解説した手法を用いることで、異なる条件下で得られたデータセット間の差異が統計的に有意であるかどうかを判断することができます。そしてこれらの方法を活用するためには適切な手法の選択と正確な実施が、信頼性の高い結果を導く鍵となります。
この記事を通じて基本的な理解を深め、実際のデータ解析に活かしていただければ幸いです。
今回は“対応のない”データを用いた分散分析・多重比較法を実際に行う方法を解説しました。分散分析・多重比較法の概要を知りたい方は下記を参照してください。
コメント