Last Updated on 2023年12月28日 by カメさん

こんにちは!看護師のカメさん(@49_kame)です。
この記事は5分程度で読めます。

今回は第1種の過誤(αエラー)や第2種の過誤(βエラー)について解説するよ。
第1種の過誤(αエラー)と第2種の過誤(βエラー)は、統計解析を行う上で基本となる知識です。知らなくても解析はできますが、解析結果を正確に解釈するためにも、理解しておきましょう。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。
第1種の過誤(αエラー)と第2種の過誤(βエラー)とは?
統計には、第1種の過誤と第2種の過誤があります。過誤とは誤りのことです。
つまり簡単に言うと、第1種の過誤と第2種の過誤とは検定結果の判定間違いの種類のことです。
第1種の過誤(αエラー)とは?
第1種の過誤は、「第1種の誤り」「type 1 error」「タイプ1のエラー」「αエラー」などと呼ばれます。
ここからは差の検定を例に解説します。
第1種の過誤(αエラー)は、本当は差がないのに「差がある」と間違って判定することです。

そして第1種の過誤が起きる確率がαです。確率αとは有意水準p のことです。有意水準pは、p=0.05や0.01に設定されます。

研究結果で良く見かけるp<0.05と言うのは第1種の過誤(差があると判定する間違い)の確率が5%以下ということです。
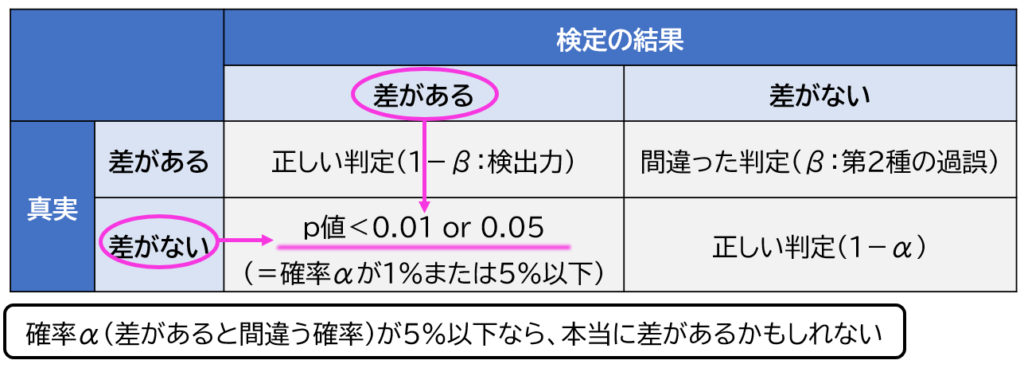
統計では有意水準pを研究者が設定して結果を判定します。例えば有意水準pを=0.05に設定した場合の結果の解釈は、「検定の結果、差があると間違える確率は5%未満(p<0.05)なので、差がある可能性が高い」と解釈されます。

統計の世界に絶対は無いよ。結果の解釈としては「差があると間違える確率(α)が5%なら、本当に差があるかもしれないね。でもまあ、5%の確率で差がないのかもしれないけどね」みたいな感じになるよ。
1 – α とは?
一方で、差がないものを正しく「差がない」と判定する確率が1一aです。

検定の結果、αエラーを起こす確率α=p=0.05ならば、1-αは、1ー0.05=0.95(95%)ということになります。これは、95%の確率で差がないものを正しく「差がない」と判定することを意味します。


1-αは、αエラーの反対だよ。つまり「正しいもの(本当に差がないもの)」を見抜く確率だと覚えよう。
第1種の過誤(αエラー)のまとめ
- 差がないときに「差がある」を間違って採沢(第1種の過誤)する確率a=有意水準p
- 差がないときに「差がない」を正しく採択する確率が1一a=0.95
- 第1種の過誤とは、検定の結果「差がある」と判定したが、本当は差がなかったという間違い
有意確率について詳しく知りたい方は下記の記事に詳しくまとめています。良かったら参照してください。
第2種の過誤(βエラー)とは?
それでは次に第2種の過誤について解説します。
第2種の過誤は「第2種の誤り」「 type 2 error」「タイプ2のエラー」「βエラー」などと呼ばれます。
第2種の過誤(βエラー)とは、本当は差があるのに「差がない」と間違って判定することです。


せっかく差がある結果なのに、差がないと言っちゃうのが第2種の過誤(βエラー)だね
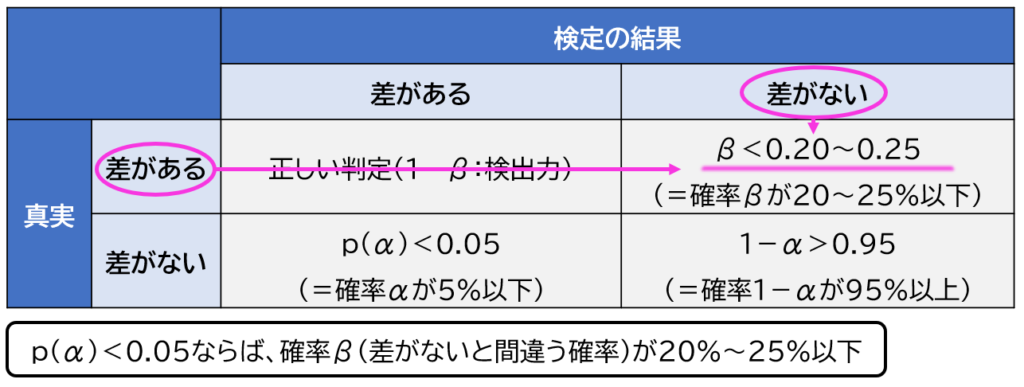
そして第2種の過誤が起きる確率がβです。確率βは一般的にβ=4〜5×αに設定されます。αは前述の通り0.05に設定されることが多いため、β=4〜5×0.05=0.20〜0.25となります
β=0.20~0.25とは20〜25%の確率で差があるのに「差がない」と判定してしまうということです。
1-β(検出力)とは?
一方で、差があるものを正しく「差がある」と判定する確率が1一βで、検出力(power)と呼ばれます。

β=0.20~0.25とすると、1ーβ=1ー0.2~0.25=0.75~0.8となります。これは、75%~80%の確率で「差がある」ものを正しく「差がある」と判定することを意味します。
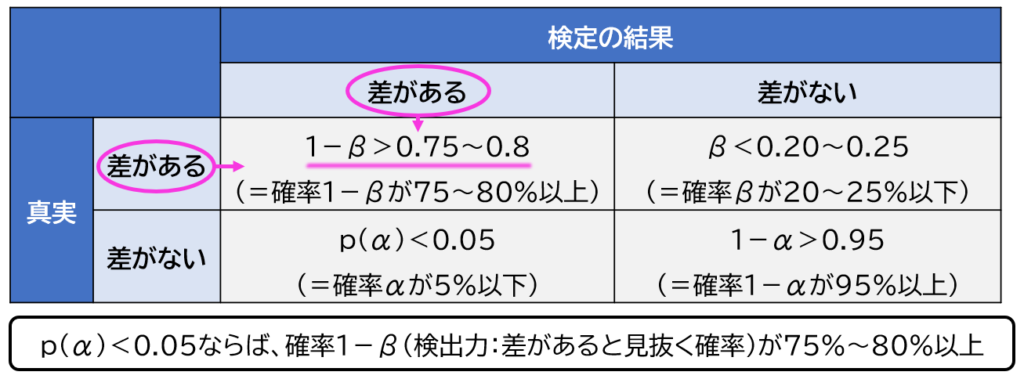

1ーβはβエラーの反対だよ。つまり正しいものを見抜く確率だね。これは検出力と呼ばれて、検定結果の判定において重要視されているよ。
第2種の過誤(βエラー)のまとめ
- 差がある時に「差がない」を間違って採沢(第2種の過誤)する確率がβ=0.20〜0.25
- 差があるときに「差がある」を正しく採択する確率が1一β=0.75~0.8
- 第2種の過誤とは、検定の結果「差がない」と判定したが、本当は差があったという間違い

「確率α」「確立β」が判定を間違う確率で、「1-α」「1-β」が正しく判定する確率だね
「1ーα」と「1ーβ(検出力)」は解析の精度を表す!
「1ーα」と「1ーβ(検出力)」は解析の精度を反映しています。
前述の通り、1ーαは「差がないものを、正しく「差がない」と見抜く確率」であり、1ーβ(検出力)は「差があるものを、正しく「差がある」と見抜く確率」です。
つまり1ーαも1ーβ(検出力)も、どちらも正しいものを見抜く力です。正しいものを見抜く力である、1ーαと1ーβが大きいほど検定の判定精度が高くなります。

検定では1ーαよりもα(=p値)の方が良く使うのでα(=p値)を用いて考えることが一般的です。1ーαが高いということは、α(=p値)が低くなります。そのため、1ーβ(検出力)が高く、α(=p値)が低いほど検定の精度が高いと言えます。


正しく判定する確率(1-β)が高くて、間違って判定する確率(α)が低いのであれば、解析の精度は高いよね。
また両者の関係では、1ーβ(検出力)が上がると反対に、α(=p値)が下がるという特性があります。検定結果を確認し、p値が低いのであれば、検出力が高いことが予想されます。そのため、低いp値が算出されていれば、判定精度が高い検定結果と言うことができます。

ちなみに、p<0.05の場合よりもp<0.01で判定されている方が判定精度は高くなるよ。
1ーβ(検出力)やα(=p値)は「差の程度」とは関係ない
1ーβ(検出力)やα(=p値)は、判定の精度を反映しますが、差の程度は反映しません。どんなに判定の精度が高くても、大きな差があるとは言えません。

p値が低いと、「差がある確率」は上がるけど、「差の大きさ」とは関係ないよ
95%信頼区間や効果量については下記の記事にまとめています。良かったら参照してください。
1ーβ(検出力)はサンプルサイズの設計に必要!
信頼性の高い研究を行うためには事前のサンプルサイズの設計が重要となります。小さなサンプルサイズだと、得られた結果が今回の対象に限定した結果なのか、母集団を反映する結果なのかが分かりません。また大きすぎるサンプルサイズは確かに、有意な差が出やすいですが、手間やコストが大きくなる問題があります。

本当は差がある介入なのに、サンプルサイズが小さすぎて差が出ないとかだったらもったいないよね。
そのため、研究の計画段階から適切なサンプルサイズを設計することが必要となります。適切なサンプルサイズの設計には前述の検出力(1ーβ)を用いた検出力分析(power analysis)が有用です。
検出力分析とは、「有意水準」と「検出力」と「サンプルサイズ」と「効果量」の4因子のうち3つの因子の値が決まると、残りの1つの因子の値が決まるという特性を利用したものです。
サンプルサイズの算出方法等の詳しい解説は下記の記事でまとめています。参照してください。
【サンプルサイズとは?】「研究に必要な対象者数の計算方法を解説!(検定力分析・区間推定)」
おまけ:「第1種の過誤・第2種の過誤」と「帰無仮説・対立仮説」の関係
おまけとして、「第1種の過誤・第2種の過誤」と「帰無仮説・対立仮説」の関係について説明します。
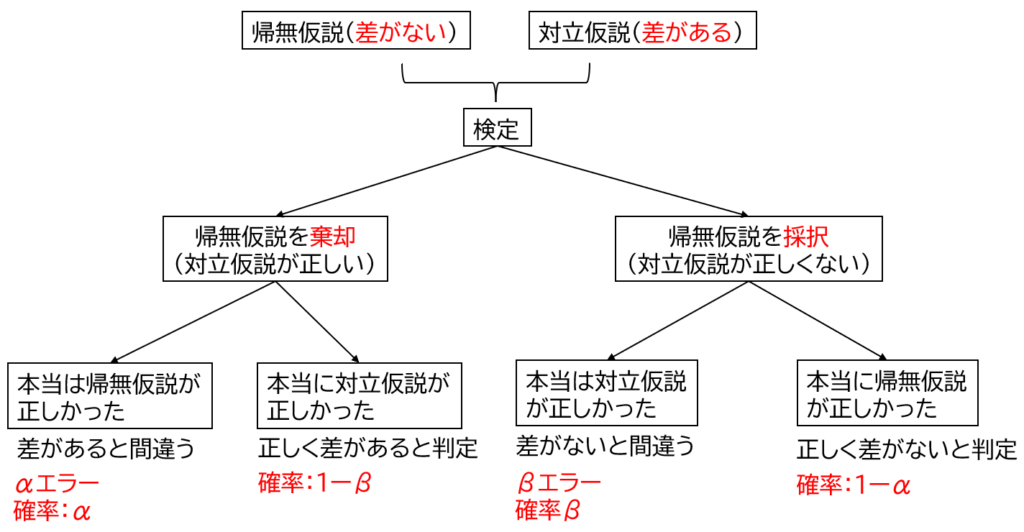
今回も引き続き、差の検定を例に解説します。統計では帰無仮説を棄却(否定)できるかどうかを判定するために検定を行います。差の検定においては、帰無仮説が「差がない」、対立仮説が「差がある」として検定を行います。帰無仮説(差がない)を棄却することができれば、対立仮説(差がある)が採択されます。つまり「差がある」という結果が示されます。
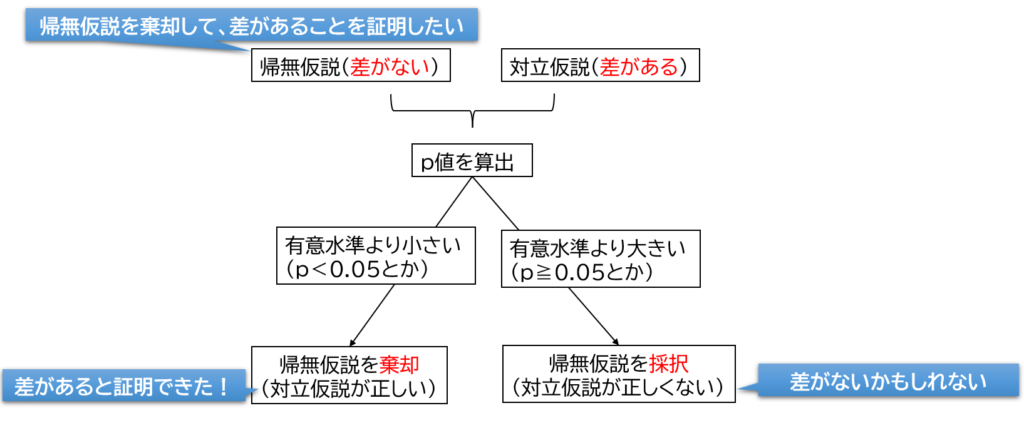

研究では帰無仮説(差がある)を棄却できたら嬉しい結果だね。
第1種の過誤(αエラー)とは、「本当は帰無仮説(差がない)が正しいはずなのに、対立仮説(差がある)を選んでしまう間違い」のことで、この確率がα(p値:有意確率)です。
反対に第2種の過誤(βエラー)とは、「本当は対立仮説(差がある)が正しいはずなのに、帰無仮説(差がない)を選んでしまう間違い」のことで、この確率がβです。
ちなみに1一β(検出力)は、「対立仮説(差がある)が成り立つときに、対立仮説(差がある)を正しく選ぶ確率」のことです。
まとめ

第1種の過誤(αエラー)と第2種の過誤(βエラー)とは、検定結果の判定を間違えてしまうことです。判定を間違う確率が、それぞれαとβです。
そして1ーαと1ーβ(検出力)が、検定結果を正しく判定する確率です。
あくまで統計は確率だと理解することが重要です。間違えることも当然あります(αエラー・βエラー)。そして間違えない確率(検出力)を高めることで、精度の高い解析となります。
検定の結果を確認する際は、今回の内容を思い出しながら解釈してみてください。

検定の結果がp<0.05でも、絶対に差があるとは言えないよ。「差がある可能性は高いが、もしかしたらp<0.05の確率で差がない(αエラー)かもしれません」としか言えないのが統計の世界だよ。
この記事を読んだ方におすすめの書籍を下記で紹介しています。良かったら参照してください。
研究では統計解析のために膨大なデータ(アンケート調査のデータなど)を入力する作業が必要となります。これは単純作業ですが、多大な労力と時間を要します。また正確性も重要になります。そのため、データ入力を専門業者に依頼することも1つの選択肢だと思います。
興味のある方は【アンケート調査のデータ入力は代行業者にお任せ】研究データのデータ入力代行業者を探すならEMEAO!(エミーオ)がおすすめ!で紹介しているので良かったら参照してください。













コメント